⊳思维建模能力的培养

⊳情景作图能力的培养

 

 

模型概述

带电粒子在周期性变化的电、磁场中的运动是高中物理的一个难点．题目中的运动情景复杂、综合性强，将场的性质、运动学规律、牛顿运动定律、功能关系以及交变电场等知识有机地结合，对空间想象能力、物理过程和运动规律的综合分析能力，以及利用数学知识解决物理问题的能力要求较高．

例1　如图1甲所示，间距为d、垂直于纸面的两平行板P、Q间存在匀强磁场、取垂直于纸面向里为磁场的正方向，磁感应强度随时间的变化规律如图乙所示．t＝0时刻，一质量为m、带电荷量为＋q的粒子(不计重力)，以初速度v₀由Q板左端靠近板面的位置，沿垂直于磁场且平行于板面的方向射入磁场区．当B₀和T_B取某些特定值时，可使t＝0时刻入射的粒子经Δt时间恰能垂直打在P板上(不考虑粒子反弹)．上述m、q、d、v₀为已知量．

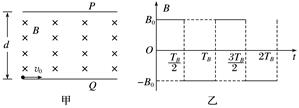
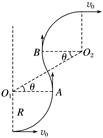
图1

(1)若Δt＝T_B，求B₀；

(2)若Δt＝T_B，求粒子在磁场中运动时加速度的大小；

(3)若B₀＝，为使粒子仍能垂直打在P板上，求T_B.

答案　(1)　(2)　(3)见解析

解析　(1)设粒子做圆周运动的半径为R₁，由牛顿第二定律得qv₀B₀＝①

根据题意由几何关系得R₁＝d②

联立①②式得B₀＝③

(2)设粒子做圆周运动的半径为R₂，加速度大小为a，由圆周运动公式得a＝④

根据题意由几何关系得3R₂＝d⑤

联立④⑤式得a＝⑥

(3)设粒子做圆周运动的半径为R，周期为T，由圆周运动公式得T＝⑦

由牛顿第二定律得qv₀B₀＝⑧

由题意知B₀＝，代入⑧式得

d＝4R⑨

粒子运动轨迹如图所示(只画出一个周期的运动情况)，O₁、O₂为圆心，O₁O₂连线与水平方向的夹角为θ，在每个T_B内，只有A、B两个位置才有可能垂直击中P板，且均要求0＜θ＜，由题意可知T＝⑩

设经历完整T_B的个数为n(n＝0,1,2,3，…)，

若A位置击中P板，根据题意由几何关系得

R＋2(R＋Rsin θ)n＝d⑪

当n＝0时，无解⑫

当n＝1时，联立⑨⑪式得θ＝(或sin θ＝)⑬

联立⑦⑨⑩⑬式得T_B＝⑭

当n≥2时，不满足0＜θ＜90°的需求⑮

若B位置击中P板，根据题意由几何关系得

R＋2Rsin θ＋2(R＋Rsin θ)n＝d⑯

当n＝0时，无解⑰

当n＝1时，联立⑨⑯式得θ＝arcsin(或sin θ＝)⑱

联立⑦⑨⑩⑱式得T_B＝(＋arcsin ).

当n≥2时，不满足0＜θ＜90°的要求．

1．仔细分析并确定各场的变化特点及相应的时间，其变化周期一般与粒子在电场或磁场中的运动周期相关联，应抓住变化周期与运动周期之间的联系作为解题的突破口．

2．必要时，可把粒子的运动过程还原成一个直观的运动轨迹草图进行分析．

3．把粒子的运动分解成多个运动阶段分别进行处理，根据每一阶段上的受力情况确定粒子的运动规律．

带电粒子在多磁场中的运动，一般是指带电粒子在两个相邻匀强磁场中的运动．解决此类问题的一般思路：

(1)根据题中所给的条件，画出粒子在两磁场中做匀速圆周运动的轨迹；

(2)根据画出的轨迹，找出粒子在两磁场中做圆周运动的圆心和半径；

(3)适当添加辅助线，运用数学方法计算出粒子在两磁场中的轨迹半径(有时候还要找出圆心角)；

(4)结合粒子运动的半径公式r＝(或周期公式T＝)即可得出所求的物理量．

例2　如图2所示，在一个圆形区域内，两个方向相反且都垂直于纸面的匀强磁场分布在以直径A₂A₄为边界的两个半圆形区域Ⅰ和Ⅱ中，直径A₂A₄与直径A₁A₃之间的夹角为α＝60°.一质量为m、电荷量为q的带正电粒子以某一速度从Ⅰ区的边缘点A₁处沿与A₁A₃成β＝30°角的方向射入磁场，随后该粒子以垂直于A₂A₄的方向经过圆心进入Ⅱ区，最后再从A₄处射出磁场．已知该粒子从射入到射出磁场所用的时间为t，求：

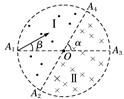
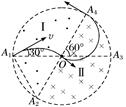
图2

(1)粒子在磁场区域Ⅰ和Ⅱ中运动的轨道半径R₁与R₂的比值；

(2)Ⅰ区和Ⅱ区中磁场的磁感应强度B₁和B₂的大小．

答案　(1)2　(2)　

解析　(1)粒子在两匀强磁场中的运动轨迹如图所示

设粒子射入磁场时的速度大小为v，圆形区域的半径为r.连接A₁A₂，由几何知识可知，△A₁A₂O为等边三角形，A₂为粒子在区域Ⅰ磁场中运动时轨迹圆的圆心，所以R₁＝r.由于粒子垂直直径A₂A₄进入Ⅱ区，从A₄点离开磁场，所以粒子在区域Ⅱ磁场中运动的轨迹为半圆，圆形磁场区域的半径OA₄即粒子在Ⅱ区磁场中做圆周运动时轨迹圆的直径，所以R₂＝，由此可得：＝2.

(2)带电粒子在Ⅰ区磁场中做圆周运动的周期为T₁＝，因为∠A₁A₂O＝60°，所以粒子在Ⅰ区磁场中运动的时间为t₁＝＝.带电粒子在Ⅱ区磁场中做圆周运动的周期为T₂＝，因粒子在Ⅱ区磁场中运动轨迹为半圆，所以其运动时间为t₂＝＝，带电粒子在磁场中运动的总时间为t＝t₁＋t₂，又因为＝2，所以B₂＝2B₁，由以上各式可得：B₁＝，B₂＝.