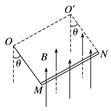
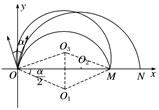
45分钟章末验收卷一、单项选择题 1.如图1所示,质量为m、长度为L的金属棒MN两端由等长的轻质细线水平悬挂在O、O′点,处于竖直向上的匀强磁场中,磁感应强度大小为B,棒中通以某一方向的电流,平衡时两细线与竖直方向夹角均为θ,重力加速度为g.则( )
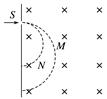
图1 A.金属棒中的电流方向由N指向M B.金属棒MN所受安培力的方向垂直于OMNO′平面向上 C.金属棒中的电流大小为tan θ D.每条细线所受拉力大小为mgcos θ 答案 C 解析 平衡时两细线与竖直方向夹角均为θ,故金属棒受到安培力,根据左手定则,可判断金属棒中的电流方向由M指向N,故A错误;金属棒MN所受安培力的方向垂直于MN和磁场方向向右,故B错误;设每条细线所受拉力大小为FT,由受力分析可知,2FTsin θ=BIL,2FTcos θ=mg,得 I=tan θ,故C正确;由受力分析可知,2FTcos θ=mg,得FT=·,故D错误. 2.不计重力的两个带电粒子M和N沿同一方向经小孔S垂直进入匀强磁场,在磁场中的径迹如图2.分别用vM与vN、tM与tN、与表示它们的速率、在磁场中运动的时间、荷质比,则( )
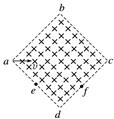
图2 A.如果=,则vM>vN B.如果=,则tM<tN C.如果vM=vN,则> D.如果tM=tN,则> 答案 A 解析 由洛伦兹力提供向心力可得qvB=m,=,由它们在磁场中的轨迹可知,两个带电粒子M和N轨迹的半径关系为rM>rN,如果=,则vM>vN,选项A正确;两个带电粒子M和N在匀强磁场中轨迹均为半个圆周,运动时间均为半个周期,由T=可知,如果=,则两个带电粒子M和N在匀强磁场中运动周期相等,tM=tN,选项B错误,同理,选项D错误;由qvB=m,可解得v=.如果vM=vN,则<,选项C错误. 3.如图3所示,有一个正方形的匀强磁场区域abcd,e是ad的中点,f是cd的中点,如果在a点沿对角线方向以速度v射入一带负电的粒子(带电粒子重力不计),恰好从e点射出,则( )
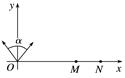
图3 A.如果粒子的速度增大为原来的2倍,将从d点射出 B.如果粒子的速度增大为原来的3倍,将从f点射出 C.如果粒子的速度不变,磁场的磁感应强度变为原来的2倍,将从d点射出 D.只改变粒子的速度使其分别从e、d、f点射出时,从e点射出所用时间最短 答案 A 解析 如果粒子的速度增大为原来的2倍,磁场的磁感应强度不变,由半径公式R=可知,半径将增大为原来的2倍,根据几何关系可知,粒子正好从d点射出,故A项正确;设正方形边长为2a,则粒子从e点射出,轨迹半径为a.磁感应强度不变,粒子的速度变为原来的3倍,则轨迹半径变为原来的3倍,即轨迹半径为a,则由几何关系可知,粒子从fd之间射出磁场,B项错;如果粒子速度不变,磁感应强度变为原来的2倍,粒子轨迹半径减小为原来的一半,因此不可能从d点射出,C项错;只改变粒子速度使其分别从e、d、f三点射出时,从f点射出时轨迹的圆心角最小,运动时间最短,D项错. 4.如图4,匀强磁场垂直于纸面,磁感应强度大小为B,某种比荷为、速度大小为v的一群离子以一定发散角α由原点O出射,y轴正好平分该发散角,离子束偏转后打在x轴上长度为L的区域MN内,则cos 为( )
图4 A.- B.1- C.1- D.1- 答案 B 解析 由洛伦兹力提供向心力得qvB=m, 解得r=. 根据题述,当离子速度方向沿y轴正方向时打在N点,当离子速度方向与y轴正方向夹角为时打在M点,画出三种情况下离子的运动轨迹如图所示,
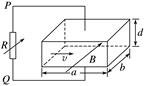
设OM之间的距离为x,则有2rcos =x,2r=x+L,联立解得cos =1-,选项B正确. 二、多项选择题 5.如图5所示,磁流体发电机的长方体发电导管的前后两个侧面是绝缘体,上下两个侧面是电阻可忽略的导电电极,两极间距为d,极板长和宽分别为a和b,这两个电极与可变电阻R相连.在垂直前后侧面的方向上有一匀强磁场,磁感应强度大小为B.发电导管内有电阻率为ρ的高温电离气体——等离子体,等离子体以速度v向右流动,并通过专用通道导出.不计等离子体流动时的阻力,调节可变电阻的阻值,则( )
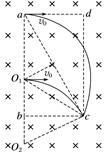
图5 A.运动的等离子体产生的感应电动势为E=Bav B.可变电阻R中的感应电流方向是从Q到P C.若可变电阻的阻值为R=ρ,则其中的电流为I= D.若可变电阻的阻值为R=ρ,则可变电阻消耗的电功率为P= 答案 CD 解析 根据左手定则,等离子体中的带正电粒子受到的洛伦兹力向上,带正电粒子累积在上极板,可变电阻R中电流方向从P到Q,B错误;当带电粒子受到的电场力与洛伦兹力平衡时,两极板间电压稳定,设产生的电动势为E,则有qvB=q,E=Bdv,A错误;发电导管内等离子体的电阻r=ρ,若可变电阻的阻值为R=ρ,由闭合电路欧姆定律有I==,可变电阻消耗的电功率P=I2R=,C、D正确. 6.如图6所示,空间中有垂直纸面向里的匀强磁场,垂直磁场方向的平面内有一长方形区域abcd,其bc边长为L,ab边长为L.两同种带电粒子(重力不计)以相同的速度v0分别从a点和ab边上的P点垂直射入磁场,速度方向垂直于ab边,两粒子都恰好经过c点,则下列说法中正确的是( )
图6 A.粒子在磁场中运动的轨道半径为L B.粒子从a点到c点的运动时间为 C.粒子的比荷为 D.P点与a点的距离为 答案 ACD 解析 如图, 连接ac,ac=2L,即为轨迹圆弧对应的弦,作弦ac的垂直平分线交ab于点O1,即为粒子从a点到c点运动轨迹的圆心,半径R==L,A正确;粒子从a点到c点的运动时间t==,B错误;由于R=,则比荷==,C正确;从P点射入的粒子的轨迹半径也等于R,根据几何关系,可以求出轨迹圆心O2点到b点的距离为=L,P点与a点的距离为L+L-L=L,P点与O1点重合,D正确.
7.如图7所示,在光滑绝缘的水平面上叠放着两个物块A和B,A带负电、质量为m、电荷量为q,B质量为2m、不带电,A和B间动摩擦因数为0.5.初始时A、B处于静止状态,现将大小为F=mg的水平恒力作用在B上,g为重力加速度.A、B处于水平向里的磁场之中,磁感应强度大小为B0.若A、B间最大静摩擦力等于滑动摩擦力,则下列说法正确的是( )
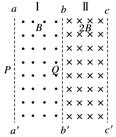
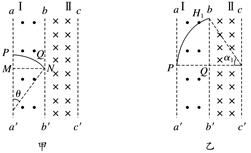
图7 A.水平力作用瞬间,A的加速度大小为 B.A做匀加速运动的时间为 C.A的最大速度为 D.B的最大加速度为g 答案 BC 解析 F作用在B上瞬间,假设A、B一起加速,则对A、B整体有F=3ma=mg,对A有FfA=ma=mg<μmg=mg,假设成立,因此A、B共同做加速运动,加速度为,A选项错误;A、B开始运动后,整体在水平方向上只受到F作用,做匀加速直线运动,对A分析,B对A有水平向左的静摩擦力FfA静作用,由FfA静=知,FfA静保持不变,但A受到向上的洛伦兹力,支持力FNA=mg-qvB0逐渐减小,最大静摩擦力μFNA减小,当FfA静=μFNA时,A、B开始相对滑动,此时有=μ(mg-qv1B0),v1=,由v1=at得t=,B正确;A、B相对滑动后,A仍受到滑动摩擦力作用,继续加速,有FfA滑=μ(mg-qvAB0),速度增大,滑动摩擦力减小,当滑动摩擦力减小到零时,A做匀速运动,有mg=qv2B0,得最大速度v2=,C选项正确;A、B相对滑动后,对B有F-FfA滑=2maB,FfA滑减小,则aB增大,当FfA滑减小到零时,aB最大,有aB==,D选项错误. 三、非选择题 8.aa′、bb′、cc′为足够长的匀强磁场分界线,相邻两分界线间距均为d,磁场方向如图8所示,Ⅰ、Ⅱ区域磁感应强度分别为B和2B,边界aa′上有一粒子源P,平行于纸面向各个方向发射速率为的带正电粒子,Q为边界bb′上一点,PQ连线与磁场边界垂直,已知粒子质量为m,电荷量为q,不计粒子重力和粒子间相互作用力,求:
图8 (1)沿PQ方向发射的粒子飞出Ⅰ区时经过bb′的位置; (2)粒子第一次通过边界bb′的位置范围; (3)进入Ⅱ区的粒子第一次在磁场Ⅱ区中运动的最长时间和最短时间. 答案 见解析 解析 (1)由洛伦兹力充当向心力得Bqv= r1= 把v=代入得r1=2d 如图甲所示sin θ==,θ=30° PM=QN=2d-2dcos θ=(2-)d 则经过bb′的位置为Q下方(2-)d处
(2)当带正电粒子速度竖直向上进入磁场Ⅰ,距离Q点上方最远,如图乙所示,由几何关系得cos α1==,α1=60° QH1=2dsin α1=d 当带正电粒子进入磁场Ⅰ后与bb′相切时,距离Q点下方最远,如图丙所示,由几何关系得cos α2==,α2=60° QH2=2dsin α2=d 粒子通过的范围长度为L=2d
(3)r2==d T== 轨迹圆所对应的弦越长,在磁场Ⅱ中运动的时间越长.如图丁所示,当轨迹圆的弦长为直径时,所对应的时间最长为tmax==
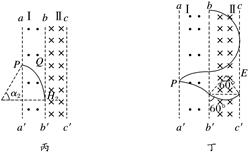
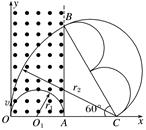
当轨迹圆的弦长为磁场Ⅱ的宽度时,从cc′飞出,所对应的时间最短为tmin== 当粒子从Q最上方进入Ⅱ区时,如图戊所示,从bb′飞出所对应的时间最短为tmin== 所以粒子第一次在磁场Ⅱ中运动的最短时间为tmin=. 9.如图9所示,在平面直角坐标系xOy内,第Ⅰ象限的等腰直角三角形MNP区域内存在垂直于坐标平面向外的匀强磁场,y<0的区域内存在着沿y轴正方向的匀强电场.一质量为m、电荷量为q的带电粒子从电场中Q(-2h,-h)点以速度v0水平向右射出,经坐标原点O处射入第Ⅰ象限,最后以垂直于PN的方向射出磁场.已知MN平行于x轴,N点的坐标为(2h,2h),不计粒子的重力,求:
图9 (1)电场强度的大小E; (2)磁感应强度的大小B; (3)粒子在磁场中运动的时间t. 答案 (1) (2) (3) 解析 (1)粒子运动轨迹如图所示,
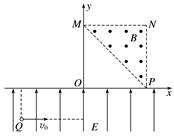
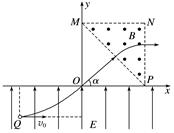
粒子在电场中运动的过程中,由平抛运动规律及牛顿运动定律得:2h=v0t h=at2 qE=ma 解得E= (2)粒子到达O点时,沿y轴正方向的分速度 vy=at=·=v0 则速度方向与x轴正方向的夹角α满足:tan α==1 即α=45° 粒子从MP的中点垂直于MP进入磁场,垂直于NP射出磁场,粒子在磁场中的速度为:v=v0 轨道半径R=h 又由qvB=m得B= (3)由T=,且由几何关系可知小粒子在磁场中运动的圆心角为45°, 故粒子在磁场中的运动时间t=·=. 10.如图10所示,在xOy平面内的第一象限内,x=4d处竖直放置一个长l=4d的粒子吸收板AB,在AB左侧存在垂直纸面向外的磁感应强度为B的匀强磁场.在原点O处有一粒子源,可沿y轴正方向射出质量为m、电荷量为q的不同速率的带正电粒子,不计粒子的重力.
图10 (1)若射出的粒子能打在AB板上,求粒子速率v的范围; (2)若在点C(8d,0)处放置一粒子回收器,在B、C间放一挡板(粒子与挡板碰撞无能量损失),为回收恰从B点进入BC右侧区间的粒子,需在BC右侧加一垂直纸面向外的匀强磁场(图中未画出),求此磁场磁感应强度的大小和此类粒子从O点发射到进入回收器所用的时间. 答案 (1)≤v≤ (2)见解析 解析 (1)粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力.
①粒子打在吸收板AB的下边界A点,设粒子的速率为v1,由图中几何关系可知圆心在O1点,粒子的轨道半径r1=2d 由牛顿第二定律可得:qv1B= 联立可得:v1= ②粒子打在吸收板AB的上边界B点,设粒子的速率为v2,由图中几何关系可知圆心在C点,粒子的轨道半径r2=8d 由牛顿第二定律可得:qv2B= 联立可得:v2= 由题意可得:若射出的粒子能打在AB板上,粒子的速率v需满足:≤v≤ (2)经过B点的粒子能够到达C点,设磁场的磁感应强度为B′,由图中几何关系,粒子的轨道半径r=(n=1,2,3,…) 由牛顿第二定律可得:qv2B′= 联立可得:B′=2nB(n=1,2,3,…) 粒子从O到B的运动时间t1== 粒子从B到C的运动时间t2=T=×= 故粒子从O到C的运动时间t=t1+t2=.
|