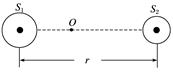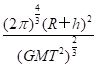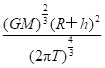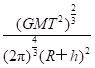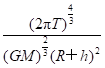专题强化五　地球同步卫星　双星或多星模型

专题解读 1.本专题是万有引力定律在天体运行中的特殊运用，同步卫星是与地球(中心)相对静止的卫星；而双星或多星模型有可能没有中心天体，近年来常以选择题形式在高考题中出现．

2．学好本专题有助于学生加深万有引力定律的灵活应用，加深力和运动关系的理解．

3．需要用到的知识：牛顿第二定律、万有引力定律、圆周运动规律等．

命题点一　地球同步卫星

1．定义：相对于地面静止且与地球自转具有相同周期的卫星叫地球同步卫星．

2．“七个一定”的特点

(1)轨道平面一定：轨道平面与赤道平面共面．

(2)周期一定：与地球自转周期相同，即T＝24 h.

(3)角速度一定：与地球自转的角速度相同．

(4)高度一定：由G＝m(R＋h)得地球同步卫星离地面的高度h＝3.6×10⁷ m.

(5)速率一定：v＝ ＝3.1×10³ m/s.

(6)向心加速度一定：由G＝ma得a＝＝g_h＝0.23 m/s²，即同步卫星的向心加速度等于轨道处的重力加速度．

(7)绕行方向一定：运行方向与地球自转方向相同．

例1　利用三颗位置适当的地球同步卫星，可使地球赤道上任意两点之间保持无线电通讯．目前，地球同步卫星的轨道半径约为地球半径的6.6倍．假设地球的自转周期变小，若仍仅用三颗同步卫星来实现上述目的，则地球自转周期的最小值约为(　　)

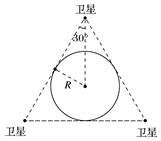
A．1 h  B．4 h  C．8 h  D．16 h

答案　B

解析　地球自转周期变小，卫星要与地球保持同步，则卫星的公转周期也应随之变小，由开普勒第三定律＝k可知卫星离地球的高度应变小，要实现三颗卫星覆盖全球的目的，则卫星周期最小时，由数学几何关系可作出它们间的位置关系如图所示．

卫星的轨道半径为r＝＝2R

由＝得

＝.

解得T₂≈4 h.

解决同步卫星问题的“四点”注意

1．基本关系：要抓住：G＝ma＝m＝mrω²＝mr.

2．重要手段：构建物理模型，绘制草图辅助分析．

3．物理规律

(1)不快不慢：具有特定的运行线速度、角速度和周期．

(2)不高不低：具有特定的位置高度和轨道半径．

(3)不偏不倚：同步卫星的运行轨道平面必须处于地球赤道平面上，只能静止在赤道上方的特定的点上．

4．重要条件

(1)地球的公转周期为1年，其自转周期为1天(24小时)，地球的表面半径约为6.4×10³ km，表面重力加速度g约为9.8 m/s².

(2)月球的公转周期约27.3天，在一般估算中常取27天．

(3)人造地球卫星的运行半径最小为r＝6.4×10³ km，运行周期最小为T＝84.8 min，运行速度最大为v＝7.9 km/s .

1．国务院批复，自2016年起将4月24日设立为“中国航天日”．如图1所示，1970年4月24日我国首次成功发射的人造卫星东方红一号，目前仍然在椭圆轨道上运行，其轨道近地点高度约为440 km，远地点高度约为2 060 km；1984年4月8日成功发射的东方红二号卫星运行在赤道上空35 786 km的地球同步轨道上．设东方红一号在远地点的加速度为a₁，东方红二号的加速度为a₂，固定在地球赤道上的物体随地球自转的加速度为a₃，则a₁、a₂、a₃的大小关系为(　　)

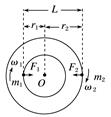
图1

A．a₂＞a₁＞a₃                                  B．a₃＞a₂＞a₁

C．a₃＞a₁＞a₂                                  D．a₁＞a₂＞a₃

答案　D

解析　由于东方红二号卫星是同步卫星，则其角速度和赤道上的物体角速度相等，根据a＝ω²r，r₂>r₃，则a₂>a₃；由万有引力定律和牛顿第二定律得，G＝ma，由题目中数据可以得出，r₁<r₂，则a₂<a₁；综合以上分析有，a₁>a₂>a₃，选项D正确．

2．研究表明，地球自转在逐渐变慢，3亿年前地球自转的周期约为22小时．假设这种趋势会持续下去，地球的其他条件都不变，未来人类发射的地球同步卫星与现在的相比(　　)

A．距地面的高度变大

B．向心加速度变大

C．线速度变大

D．角速度变大

答案　A

解析　地球的自转周期变大，则地球同步卫星的公转周期变大．由＝m(R＋h)，得h＝ －R，T变大，h变大，A正确．

由＝ma，得a＝，r增大，a减小，B错误．

由＝，得v＝ ，r增大，v减小，C错误．

由ω＝可知，角速度减小，D错误．

3．(多选)地球同步卫星离地心的距离为r，运行速率为v₁，加速度为a₁，地球赤道上的物体随地球自转的向心加速度为a₂，地球的第一宇宙速度为v₂，半径为R，则下列比例关系中正确的是(　　)

A.＝                                           B.＝()²

C.＝                                           D.＝

答案　AD

解析　设地球的质量为M，同步卫星的质量为m₁，在地球表面绕地球做匀速圆周运动的物体的质量为m₂，根据向心加速度和角速度的关系有a₁＝ωr，a₂＝ωR，又ω₁＝ω₂，故＝，选项A正确；由万有引力定律和牛顿第二定律得G＝m₁，G＝m₂，解得＝，选项D正确．

命题点二　双星或多星模型

1．双星模型

(1)定义：绕公共圆心转动的两个星体组成的系统，我们称之为双星系统，如图2所示．

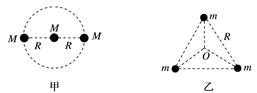
图2

(2)特点：

①各自所需的向心力由彼此间的万有引力相互提供，即

＝m₁ωr₁，＝m₂ωr₂

②两颗星的周期及角速度都相同，即

T₁＝T₂，ω₁＝ω₂

③两颗星的半径与它们之间的距离关系为：r₁＋r₂＝L

(3)两颗星到圆心的距离r₁、r₂与星体质量成反比，即＝.

2．多星模型

(1)定义：所研究星体的万有引力的合力提供做圆周运动的向心力，除中央星体外，各星体的角速度或周期相同．

(2)三星模型：

①三颗星位于同一直线上，两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图3甲所示)．

②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)．

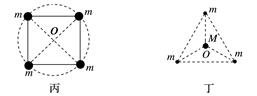
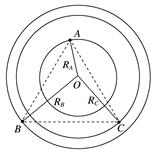
图3

(3)四星模型：

①其中一种是四颗质量相等的恒星位于正方形的四个顶点上，沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙所示)．

②另一种是三颗恒星始终位于正三角形的三个顶点上，另一颗位于中心O，外围三颗星绕O做匀速圆周运动(如图丁所示)．

例2　由三颗星体构成的系统，忽略其他星体对它们的作用，存在着一种运动形式，三颗星体在相互之间的万有引力作用下，分别位于等边三角形的三个顶点上，绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图4为A、B、C三颗星体质量不相同时的一般情况)．若A星体质量为2m、B、C两星体的质量均为m，三角形的边长为a，求：

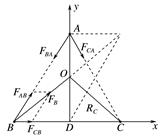
图4

(1)A星体所受合力大小F_A；

(2)B星体所受合力大小F_B；

(3)C星体的轨道半径R_C；

(4)三星体做圆周运动的周期T.

答案　(1)2G　(2)G　(3)a　(4)π

解析　(1)由万有引力定律，A星体所受B、C星体引力大小为F_BA＝G＝G＝F_CA

方向如图所示

则合力大小为F_A＝F_BA·cos 30°＋F_CA·cos 30°＝2G

(2)同上，B星体所受A、C星体引力大小分别为

F_AB＝G＝G

F_CB＝G＝G

方向如图所示，

由余弦定理得合力为：

F_B＝＝G

(3)由于m_A＝2m，m_B＝m_C＝m

通过分析可知，圆心O在BC的中垂线AD的中点

则R_C＝ ＝a

(4)三星体运动周期相同，对C星体，由F_C＝F_B＝G＝m()²R_C，可得T＝π .

4．双星系统由两颗恒星组成，两恒星在相互引力的作用下，分别围绕其连线上的某一点做周期相同的匀速圆周运动．研究发现，双星系统演化过程中，两星的总质量、距离和周期均可能发生变化．若某双星系统中两星做圆周运动的周期为T，经过一段时间演化后，两星总质量变为原来的k倍，两星之间的距离变为原来的n倍，则此时圆周运动的周期为(　　)

A.T                                          B.T

C.T                                          D.T

答案　B

解析　设两恒星的质量分别为m₁、m₂，距离为L，

双星靠彼此的引力提供向心力，则有

G＝m₁r₁

G＝m₂r₂

并且r₁＋r₂＝L

解得T＝2π

当两星总质量变为原来的k倍，两星之间距离变为原来的n倍时

T′＝2π＝·T

故选项B正确．

5．银河系的恒星中大约四分之一是双星．如图5所示，某双星由质量不等的星体S₁和S₂构成，两星在相互之间的万有引力作用下绕两者连线上某一定点O做匀速圆周运动．由天文观察测得它们的运动周期为T，若已知S₁和S₂的距离为r，引力常量为G，求两星的总质量M.

图5

答案　

解析　设星体S₁、S₂的质量分别为m₁、m₂，运动的轨道半径分别为R₁、R₂，则运动的角速度为ω＝

根据万有引力定律和向心力公式有

G＝m₁ω²R₁＝m₂ω²R₂

又R₁＋R₂＝r

联立解得两星的总质量为

M＝m₁＋m₂＝＋＝＝.

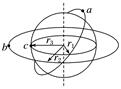
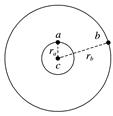
一、近地卫星、同步卫星和赤道上随地球自转的物体的比较

如图6所示，a为近地卫星，半径为r₁；b为同步卫星，半径为r₂；c为赤道上随地球自转的物体，半径为r₃.

图6

 

二、卫星追及相遇问题

典例　(多选)如图7所示，三个质点a、b、c的质量分别为m₁、m₂、M(M远大于m₁及m₂)，在c的万有引力作用下，a、b在同一平面内绕c沿逆时针方向做匀速圆周运动，已知轨道半径之比为r_a∶r_b＝1∶4，则下列说法中正确的有(　　)

图7

A．a、b运动的周期之比为T_a∶T_b＝1∶8

B．a、b运动的周期之比为T_a∶T_b＝1∶4

C．从图示位置开始，在b转动一周的过程中，a、b、c共线12次

D．从图示位置开始，在b转动一周的过程中，a、b、c共线14次

点评　某星体的两颗卫星之间的距离有最近和最远之

分，但它们都处在同一条直线上，由于它们的轨道不是重合的，因此在最近和最远的相遇问题上不能通过位移或弧长相等来处理，而是通过卫星运动的圆心角来衡量，若它们初始位置在同一直线上，实际上内轨道所转过的圆心角与外轨道所转过的圆心角之差为π的整数倍时就是出现最近或最远的时刻，而本题中a、b、c三个质点初始位置不在一条直线上，故在列式时要注意初始角度差．

答案　AD

解析　根据开普勒第三定律：周期的平方与半径的三次方成正比，则周期之比为1∶8，A对；设图示位置夹角为θ<，b转动一周(圆心角为2π)的时间为t＝T_b，则a、b相距最远时：T_b－T_b＝(π－θ)＋n·2π(n＝0,1,2,3，…)，可知n<6.75，n可取7个值；a、b相距最近时：T_b－T_b＝(2π－θ)＋m·2π(m＝0,1,2,3，…)，可知m<6.25，m可取7个值，故在b转动一周的过程中，a、b、c共线14次，D对．

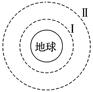
题组1　同步卫星

1．(多选)据报道，北斗卫星导航系统利用其定位、导航等功能加入到马航MH370失联客机搜救工作，为指挥中心调度部署人力、物力提供决策依据，保证了搜救船只准确抵达相关海域，帮助搜救船只规划搜救航线，避免搜救出现遗漏海域，目前北斗卫星导航定位系统由高度均约为36 000 km的5颗静止轨道卫星和5颗倾斜地球同步轨道卫星以及高度约为21 500 km的4颗中轨道卫星组网运行，下列说法正确的是(　　)

A．中轨道卫星的周期比同步卫星的周期大

B．所有卫星均位于以地心为中心的圆形轨道上

C．同步卫星和中轨道卫星的线速度均小于第一宇宙速度

D．赤道上随地球自转的物体的向心加速度比同步卫星的向心加速度大

答案　BC

解析　由开普勒第三定律可知，轨道半径较小的中轨道卫星的周期比同步卫星的周期小，A项错；由题意知，北斗导航系统的卫星轨道高度一定，因此卫星均位于以地心为中心的圆形轨道上，B项正确；第一宇宙速度是卫星绕地球的最大运行速度，C项正确；赤道上物体与同步卫星的角速度相同，由a＝ω²r可知，同步卫星的向心加速度较大，D项错．

2．如图1所示，轨道Ⅰ是近地气象卫星轨道，轨道Ⅱ是地球同步卫星轨道，设卫星在轨道Ⅰ和轨道Ⅱ上都绕地心做匀速圆周运动，运行的速度大小分别是v₁和v₂，加速度大小分别是a₁和a₂，则(　　)

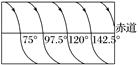
图1

A．v₁>v₂　a₁<a₂

B．v₁>v₂　a₁>a₂

C．v₁<v₂　a₁<a₂

D．v₁<v₂　a₁>a₂

答案　B

解析　根据G＝m＝ma，可知v＝ ，a＝，所以v₁>v₂，a₁>a₂.选项B正确．

3．设地球的质量为M，半径为R，自转周期为T，引力常量为G.“神舟九号”绕地球运行时离地面的高度为h，则“神舟九号”与“同步卫星”各自所在轨道处的重力加速度的比值为(　　)

A.                            B.

C.                             D.

答案　C

解析　设“神舟九号”与“同步卫星”各自所在轨道处的重力加速度分别为g_神九、g_同步，则m_神九g_神九＝G，m_同步g_同步＝G＝，联立可得＝，故C正确．

4．“神舟八号”飞船绕地球做匀速圆周运动时，飞行轨道在地球表面的投影如图2所示，图中标明了飞船相继飞临赤道上空所对应的地面的经度．设“神舟八号”飞船绕地球飞行的轨道半径为r₁，地球同步卫星飞行轨道半径为r₂.则r∶r等于(　　)

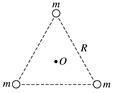
图2

A．1∶24                                         B．1∶156

C．1∶210                                       D．1∶256

答案　D

解析　从图象中可以看出，飞船每运行一周，地球自转22.5°，故飞船的周期为T₁＝×24 h＝1.5 h，同步卫星的周期为24 h，由开普勒第三定律可得＝＝()²＝，故选D.

题组2　双星、多星模型

5．(多选)宇宙间存在一些离其他恒星较远的三星系统，其中有一种三星系统如图3所示，三颗质量均为m的星位于等边三角形的三个顶点，三角形边长为R，忽略其他星体对它们的引力作用，三星在同一平面内绕三角形中心O做匀速圆周运动，万有引力常量为G，则(　　)

图3

A．每颗星做圆周运动的线速度为

B．每颗星做圆周运动的角速度为

C．每颗星做圆周运动的周期为2π

D．每颗星做圆周运动的加速度与三星的质量无关

答案　ABC

解析　由图可知，每颗星做匀速圆周运动的半径r＝＝R.由牛顿第二定律得·2cos 30°＝m＝mω²r＝mr＝ma，可解得v＝ ，ω＝ ，T＝2π，a＝，故A、B、C均正确，D错误．

6．2016年2月11日，美国科学家宣布探测到引力波的存在，引力波的发现将为人类探索宇宙提供新视角，这是一个划时代的发现．在如图4所示的双星系统中，A、B两个恒星靠着相互之间的引力正在做匀速圆周运动，已知恒星A的质量为太阳质量的29倍，恒星B的质量为太阳质量的36倍，两星之间的距离L＝2×10⁵ m，太阳质量M＝2×10³⁰ kg，引力常量G＝6.67×10^－11 N·m²/kg²，π²＝10.若两星在环绕过程中会辐射出引力波，该引力波的频率与两星做圆周运动的频率具有相同的数量级，则根据题目所给信息估算该引力波频率的数量级是(　　)

图4

A．10² Hz  B．10⁴ Hz  C．10⁶ Hz  D．10⁸ Hz

答案　A

解析　A、B的周期相同，角速度相等，靠相互之间的引力提供向心力，

有G＝M_Ar_A①

G＝M_Br_B②

有M_Ar_A＝M_Br_B，r_A＋r_B＝L，

解得r_A＝L＝L＝L.

由①得T＝ ，

则f＝＝ ＝ Hz≈1.6×10² Hz.

7．经过用天文望远镜长期观测，人们在宇宙中已经发现了许多双星系统，通过对它们的研究，使我们对宇宙中物质的存在形式和分布情况有了较深刻的认识，双星系统由两个星体组成，其中每个星体的线度都远小于两星体之间的距离，一般双星系统距离其他星体很远，可以当成孤立系统来处理．现根据对某一双星系统的测量确定，该双星系统中每个星体的质量都是M，两者相距L，它们正围绕两者连线的中点做圆周运动．

(1)计算出该双星系统的运动周期T；

(2)若该实验中观测到的运动周期为T_观测，且T_观测∶T＝1∶(N>1)．为了理解T_观测与T的不同，目前有一种流行的理论认为，在宇宙中可能存在一种望远镜观测不到的暗物质．作为一种简化模型，我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质．若不考虑其他暗物质的影响，根据这一模型和上述观测结果确定该星系间这种暗物质的密度．

答案　(1)πL　(2)

解析　(1)双星均绕它们连线的中点做圆周运动，万有引力提供向心力，则G＝M²·，解得T＝πL.

(2)N>1，根据观测结果，星体的运动周期为T_观测＝T<T，这是由于双星系统内(类似一个球体)均匀分布的暗物质引起的，均匀分布在双星系统内的暗物质对双星系统的作用与一个质点(质点的质量等于球内暗物质的总质量M′且位于中点O处)的作用等效，考虑暗物质作用后双星系统的运动周期，即

G＋G＝M²·，

代入T＝πL并整理得M′＝M.

故所求的暗物质密度为ρ＝＝.