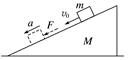
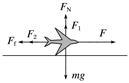
45分钟章末验收卷一、单项选择题 1.质量为M的三角形物块放置在粗糙水平地面上,开始时质量为m的物体以速度v0沿三角形物块的粗糙斜面匀速下滑,某时刻给物体施加一沿斜面向下的推力F,使物体沿斜面向下做加速运动,如图1所示.整个过程中,三角形物块始终静止在地面上,设物体向下加速运动时,地面对三角形物块的支持力大小为FN,地面对三角形物块的摩擦力的大小为Ff,重力加速度为g,则( )
图1 A.Ff≠0,FN>(m+M)g B.Ff=0,FN=(m+M)g C.Ff≠0,FN<(m+M)g D.Ff=0,FN>(m+M)g 答案 B 解析 开始时物体以速度v0沿三角形物块的粗糙斜面匀速下滑,说明三角形物块对物体的作用力等于物体的重力,方向竖直向上.对三角形物块受力分析,受到竖直向下的重力、物体对三角形物块竖直向下的作用力、地面的支持力,不受地面的摩擦力作用,根据平衡条件可知,Ff1=0,FN1=(m+M)g.当给物体施加一沿斜面向下的推力F时,不会改变物体与三角形物块间的作用力,所以地面对三角形物块的支持力大小FN=(m+M)g,地面对三角形物块的摩擦力的大小为Ff=0,选项B正确. 2.如图2所示,小球A质量为m,木块B质量为2m,两物体通过轻弹簧连接竖直放置在水平面上静止.现对A施加一个竖直向上的恒力F,使小球A在竖直方向上运动,经弹簧原长时小球A速度恰好最大,已知重力加速度为g.则在木块B对地面压力为零时,小球A的加速度大小为( )
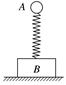
图2 A.3g B.1.5g C.2g D.2.5g 答案 C 解析 根据题意,当弹簧处于原长时A球速度最大,则F=mg,当木块B对地面压力为零时,弹簧处于伸长状态,对B受力分析,此时有kx=2mg,对A根据牛顿运动定律有kx+mg-F=ma,解得a=2g,C项正确. 3.如图3所示,光滑水平面上放置质量分别为m、2m和3m的三个木块,其中质量为2m和3m的木块间用一不可伸长的轻绳相连,轻绳能承受的最大拉力为FT.现用水平拉力F拉质量为3m的木块,使三个木块以同一加速度运动,则以下说法正确的是( )
图3 A.质量为2m的木块受到四个力的作用 B.当F逐渐增大到FT时,轻绳刚好被拉断 C.当F逐渐增大到1.5FT时,轻绳还不会被拉断 D.轻绳刚要被拉断时,质量为m和2m的木块间的摩擦力为FT 答案 C 解析 质量为2m的木块受五个力的作用,A项错;当绳的拉力为FT时,对m和2m有FT=3ma,此时对整体有F=6ma,可得F=2FT,故B项错,C项正确;轻绳刚要被拉断时,质量为m和2m的木块间的摩擦力为FT,故D项错. 4.如图4甲所示,倾角为θ的粗糙斜面体固定在水平面上,初速度为v0=10 m/s、质量为m=1 kg的小木块沿斜面上滑,若从此时开始计时,整个过程中小木块速度的平方随路程变化的关系图象如图乙所示,取g=10 m/s2,则下列说法不正确的是( )
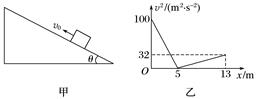
图4 A.0~5 s内小木块做匀减速运动 B.在t=1 s时刻,摩擦力反向 C.斜面倾角θ=37° D.小木块与斜面间的动摩擦因数为0.5 答案 A 解析 由匀变速直线运动的速度位移公式得v2-v=2ax,由题图乙可得a==-10 m/s2,故减速运动时间:t==1 s,故A错误;由题图乙可知,在0~1 s内小木块向上做匀减速运动,1 s后小木块反向做匀加速运动,t=1 s时摩擦力反向,故B正确;由题图乙可知,小木块反向加速运动时的加速度:a′== m/s2=2 m/s2,由牛顿第二定律得:mgsin θ+μmgcos θ=m|a|,mgsin θ-μmgcos θ=ma′,代入数据解得:μ=0.5,θ=37°,故C、D正确. 二、多项选择题 5.竖直上抛一小球,空气阻力大小恒定,小球运动的速度图象如图5所示,下列判断正确的是( )
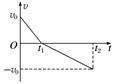
图5 A.0~t2时间内,小球的平均速度不为零 B.t1~t2时间内,小球始终在抛出点下方 C.t2时刻,小球落回抛出点 D.t2时刻,小球距离抛出点 答案 AD 解析 从图象看,0~t2时间内,小球的位移即对应速度图象中的总面积不为0,所以平均速度不为0,A项正确;t1~t2时间内,小球从最高点下落,前一段在抛出点的上方,后一段在抛出点的下方,B、C项错误;0~t1时间内,小球在抛出点上方的位移为x上=t1,t1~t2时间内,小球下落过程中的位移为x下=(t2-t1),所以总位移大小为(t2-t1)-t1=,D项正确. 6.一质量为m的飞机在水平跑道上准备起飞,受到竖直向上的机翼升力,大小与飞机运动的速率平方成正比,记为F1=k1v2;所受空气阻力也与速率平方成正比,记为F2=k2v2.假设轮胎和地面之间的阻力是压力的μ倍(μ<0.25),若飞机在跑道上加速滑行时发动机推力恒为其自身重力的0.25倍.在飞机起飞前,下列说法正确的是( ) A.飞机一共受5个力的作用 B.飞机可能做匀加速直线运动 C.飞机的加速度可能随速度的增大而增大 D.若飞机做匀加速运动,则水平跑道长度必须大于 答案 BC 解析 对飞机受力分析,受到重力、支持力、机翼的升力、发动机的推力、空气阻力和地面的摩擦力六个力的作用如图所示,A项错误;根据牛顿第二定律有:
水平方向:F-Ff-F2=ma① 竖直方向:FN+F1=mg② Ff=μFN③ 且F1=k1v2④ F2=k2v2⑤ 联立①~⑤得:F-k2v2-μ(mg-k1v2)=ma整理得 F-μmg+(μk1-k2)v2=ma⑥ 当k2=μk1时,合力恒定,加速度恒定,做匀加速直线运动,B项正确;当μk1>k2时,加速度随速度的增大而增大,C项正确;若做匀加速直线运动,由⑥式得 a==(0.25-μ)g⑦ 刚起飞时,支持力FN=0,地面摩擦力为0,mg=k1v2,得飞机刚起飞时速度的平方为:v2=⑧ v2=2ax⑨ 联立⑦⑧⑨解得x=,D项错误. 三、非选择题 7.用如图6所示的实验装置做“探究加速度与力、质量的关系”实验:
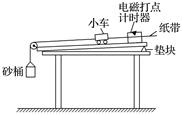
图6 (1)下面列出了一些实验器材:电磁打点计时器、纸带、带滑轮的长木板、垫块、小车和砝码、砂和砂桶.除以上器材外,还需要的实验器材有:________. A.天平(附砝码) B.秒表 C.刻度尺(最小刻度为mm) D.低压交流电源 (2)实验中,需要平衡小车和纸带运动过程中所受的阻力,正确的做法是( ) A.小车放在木板上,把木板一端垫高,调节木板的倾斜程度,使小车在不受绳的拉力时沿木板做匀速直线运动 B.小车放在木板上,挂上砂桶,把木板一端垫高,调节木板的倾斜程度,使小车在砂桶的作用下沿木板做匀速直线运动 C.小车放在木板上,后面固定一条纸带,纸带穿过打点计时器.把木板一端垫高,调节木板的倾斜程度,使小车在不受绳的拉力时能拖动纸带沿木板做匀速直线运动 (3)实验中,为了保证砂和砂桶所受的重力近似等于使小车做匀加速运动的拉力,砂和砂桶的总质量m与小车和车上砝码的总质量M之间应满足的条件是__________________.这样,在改变小车上砝码的质量时,只要砂和砂桶质量不变,就可以认为小车所受拉力几乎不变. (4)如图7为某次实验纸带,在相邻两计数点间都有四个打点未画出,用刻度尺测得:x1=0.55 cm,x2=0.94 cm,x3=1.35 cm,x4=1.76 cm,x5=2.15 cm,x6=2.54 cm.
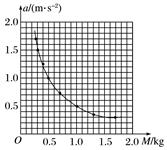
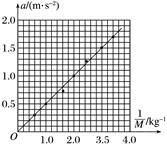
图7 ①相邻两计数点间的时间间隔为________ s; ②计数点“6”和“7”间的位移x7比较接近于________(填“A、B、C、D”序号) A.2.76 cm B.2.85 cm C.2.96 cm D.3.03 cm ③打下“3”点时小车的瞬时速度v3=________ m/s;小车的加速度a=________ m/s2.(计算结果均保留2位有效数字) (5)某小组在研究“外力一定时,加速度与质量的关系”时,保持砂和砂桶质量不变,改变小车质量M,分别记录小车加速度a与其质量M的数据.在分析处理数据时,该组同学产生分歧:甲同学认为根据实验数据可以作出小车加速度a与其质量M的图象,如图8,然后由图象直接得出a与M成反比.乙同学认为应该继续验证a与其质量倒数是否成正比,并作出小车加速度a与其质量倒数的图象,如图9所示.你认为________同学(选填“甲”或“乙”)的方案更合理.
图8
图9 (6)另一小组在研究“小车质量一定时,加速度与质量的关系”时,用改变砂的质量的办法来改变对小车的作用力F,然后根据测得的数据作出a-F图象,如图10所示.发现图象既不过原点,末端又发生了弯曲,可能原因是( )
图10 A.平衡摩擦力时,木板的倾斜角度过大,且砂和砂桶的质量较大 B.平衡摩擦力时,木板的倾斜角度过小,且砂和砂桶的质量较大 C.没有平衡摩擦力,且小车质量较大 D.平衡摩擦力时,木板的倾斜角度过小,且小车质量较大 答案 (1)ACD (2)C (3)m≪M (4)①0.1 ②C ③0.16 0.40 (5)乙 (6)B 解析 (1)本实验的目的是探究加速度与力、质量的关系,用砂桶的重力代表小车受到的合外力,需要用天平测砂桶和小车的质量,故选A项;电磁打点计时器的工作电源为低压交流电源(4~6 V),工作频率为50 Hz,周期为0.02 s,可以计时,不需要秒表,故选D项,不选B项;打点计时器打下纸带,需用刻度尺测量距离,以求加速度和瞬时速度,故选C项. (2)平衡摩擦力的方法是用重力沿斜面向下的分力来抵消摩擦力的作用,具体做法是:将小车轻放(静止)在长木板上,挂好纸带(纸带和电磁打点计时器的限位孔之间有摩擦力)、不挂砂桶,将长木板靠近打点计时器的一端适当垫高,形成斜面,轻推小车,使小车做匀速运动(纸带上两点间距离相等)即可,故C正确. (3)砂桶和小车一起运动,根据牛顿第二定律,对砂桶:mg-F=ma,对小车:F=Ma,可得小车受到的拉力F=,加速度a=,本实验用砂和砂桶的总重力代表小车受到的合外力(拉力),由F=·mg=可知,F<mg,只有m≪M时,才有F≈mg,所以砂和砂桶的总质量m与小车和车上砝码的总质量M之间应满足的条件是m≪M. (4)①打点计时器的工作周期为T0=0.02 s,相邻两计数点间都有四个打点未画出,所以两计数点之间的时间间隔为T=5T0=0.1 s. ②根据匀变速直线运动的规律a===,可知:x7=2x6-x5=2×2.54 cm-2.15 cm=2.93 cm,比较接近于2.96 cm,故选C项. ③v3=≈0.16 m/s, a=≈0.40 m/s2. (5)反比关系不容易根据图象判定,而正比关系容易根据图象判定,故应该建立小车加速度a与小车质量的倒数关系图象,故应选乙方案. (6)图象与横轴相交,说明需要用拉力平衡摩擦力,即没有平衡摩擦力或平衡摩擦力不够;由(3)可知,小车受到的拉力F=,当m≪M时,即砂和砂桶总重力远小于小车及车上砝码的总重力,绳子的拉力近似等于砂和砂桶的总重力,小车的加速度a与拉力F成正比,如果砂和砂桶的总质量太大,小车受到的拉力明显小于砂和砂桶总重力,加速度与砂和砂桶总重力(小车受到的合力)不成正比,a-F图象发生弯曲,不再是直线,故B正确. 8.如图11所示,一长L=2 m、质量M=4 kg的薄木板(厚度不计)静止在粗糙的水平台面上,其右端距平台边缘l=5 m,木板的正中央放有一质量为m=1 kg的物块(可视为质点),已知木板与平台、物块与木板间的动摩擦因数均为μ1=0.4.现对木板施加一水平向右的恒力F,其大小为48 N,g取10 m/s2,试求:
图11 (1)F作用了1.2 s时,木板的右端离平台边缘的距离; (2)要使物块最终不能从平台上滑出去,则物块与平台间的动摩擦因数μ2应满足的条件. 答案 (1)0.64 m (2)μ2≥0.2 解析 (1)假设开始时物块与木板会相对滑动,由牛顿第二定律: 对木板:F-μ1(M+m)g-μ1mg=Ma1, 解得a1=6 m/s2 对物块:μ1mg=ma2, 解得a2=4 m/s2,故假设成立 设F作用t时间后,物块恰好从木板左端滑离,则 =a1t2-a2t2,解得t=1 s 在此过程:木板位移x1=a1t2=3 m, 末速度v1=a1t=6 m/s 物块位移x2=a2t2=2 m,末速度v2=a2t=4 m/s 在物块从木板上滑落后的t0=0.2 s内,由牛顿第二定律: 对木板:F-μ1Mg=Ma1′, 解得a1′=8 m/s2 木板发生的位移x1′=v1t0+a1′t=1.36 m 此时木板右端距平台边缘Δx=l-x1-x1′=0.64 m (2)物块滑至平台后,做匀减速直线运动,由牛顿第二定律: 对物块:μ2mg=ma2′, 解得a2′=μ2g 若物块在平台上速度减为0,则通过的位移x2′= 要使物块最终不会从平台上掉下去需满足l+≥x2+x2′ 联立解得μ2≥0.2.
|