⊳规范表达能力的培养
⊳迁移变通能力的培养
规范答题要求：必要过程的叙述、遵循规律的叙述、假设物理量的叙述.
|
经典案例
|
审题流程
|
|
 例1 如图1所示，A、B为两块平行金属板，A板带正电、B板带负电．两板之间存在着匀强电场，两板间距为d、电势差为U，在B板上开有两个间距为L的小孔．C、D为两块同心半圆形金属板，圆心都在贴近B板的O′处，C带正电、D带负电．两板间的距离很近，两板末端的中心线正对着B板上的小孔，两板间的电场强度可认为大小处处相等，方向都指向O′.半圆形金属板两端与B板的间隙可忽略不计．现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电荷量为q的带正电微粒(微粒的重力不计)，求：
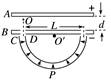
图1
(1)微粒穿过B板小孔时的速度多大？
(2)为了使微粒能在C、D板间运动而不碰板，C、D板间的电场强度大小应满足什么条件？
(3)从释放微粒开始，经过多长时间微粒会通过半圆形金属板间的最低点P点？
|
|
|
满分规范
|
评分细则·答题规则
|
|
(1)设微粒穿过B板小孔时的速度为v，根据动能定理得
qU＝mv2①(3分)
解得：v＝ (2分)
(2)微粒进入半圆形金属板后，电场力提供向心力，由牛顿第二定律得：qE＝m＝m②(3分)
联立①②解得：E＝(2分)
(3)微粒从释放开始经t1射入B板的小孔，则：
d＝vt1③(2分)
解得：t1＝2d(1分)
设微粒在半圆形金属板间运动经过t2第一次到达最低点P点，则：t2＝·＝＝ ④(2分)
从释放微粒开始到微粒第一次到达P点经过的时间：
t1＋t2＝(2d＋) ⑤(2分)
根据运动的对称性可知，再经过2(t1＋t2)时间微粒再一次经过P点，所以微粒经过P点的时间：
t＝(2k＋1)(2d＋) (k＝0、1、2……)⑥(3分)
|
第一问：
(1)只列出①式，没能计算出结果，只得3分．
(2)不列①式，而列出的是q＝ma和v2＝2ad也可得3分，计算结果正确再得2分．
答题规则：题目中已有物理量符号，一定要用题目中的字母表达方程，否则计算结果容易出现错误，影响步骤分．
第二问：
(1)不列②式，而列出的是qE＝m和L＝2R也可得3分．
(2)如果只列qE＝m，没有列出L与R的关系式，计算结果正确，扣1分，如果计算结果错误，只得2分．
答题规则：解题过程中，必要的几何关系即使简单也不能少，否则将会失去步骤分．
第三问：
(1)只列出③式，没有计算出结果，但最终结果正确，不扣分，计算结果错误，只得2分．
(2)没有列出④式，而列出的是T＝和t2＝T，最终结果正确，不扣分，计算结果错误，只得1分．
(3)没有考虑到运动的周期性，但说明了再经过2(t1＋t2)时间微粒再一次经过P点，且结果正确，可得1分．
答题规则：在时间比较紧张的情况下，要尽量根据题设条件写出必要的方程，力争多得步骤分.
|
“等效法”在电场中的应用
处理带电粒子在“等效力场”中的运动，要关注以下两点：一是对带电粒子进行受力分析时，注意带电粒子受到的电场力的方向与运动方向所成的夹角是锐角还是钝角，从而决定电场力做功情况；二是注意带电粒子的初始运动状态．
1．等效重力法．将重力与电场力
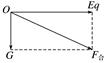
图2
进行合成，如图2所示，则F合为等效重力场中的“重力”，g′＝为等效重力场中的“等效重力加速度”，F合的方向等效为“重力”的方向，即在等效重力场中的竖直向下方向．
2．物理最高点与几何最高点．在“等效力场”做圆周运动的小球，经常遇到小球在竖直平面内做圆周运动的临界速度问题．小球能维持圆周运动的条件是能过最高点，而这里的最高点不一定是几何最高点，而应是物理最高点．
例2
如图3所示，在竖直边界线O1O2左侧空间存在一竖直向下的匀强电场，电场强度E＝100 N/C，电场区域内有一固定的粗糙绝缘斜面AB，其倾角为30°，A点距水平地面的高度为h＝4 m．BC段为一粗糙绝缘平面，其长度为L＝ m．斜面AB与水平面BC由一段极短的光滑小圆弧连接(图中未标出)，竖直边界线O1O2右侧区域固定一半径为R＝0.5 m的半圆形光滑绝缘轨道，CD为半圆形光滑绝缘轨道的直径，C、D两点紧贴竖直边界线O1O2，位于电场区域的外部(忽略电场对O1O2右侧空间的影响)．现将一个质量为m＝1 kg、电荷量为q＝0.1 C的带正电的小球(可视为质点)在A点由静止释放，且该小球与斜面AB和水平面BC间的动摩擦因数均为μ＝.求：(g取10 m/s2)
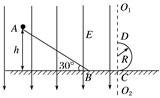
图3
(1)小球到达C点时的速度大小；
(2)小球到达D点时所受轨道的压力大小；
(3)小球落地点距离C点的水平距离．
答案 (1)2 m/s (2)30 N (3) m
解析 (1)以小球为研究对象，由A点至C点的运动过程中，根据动能定理可得
(mg＋Eq)h－μ(mg＋Eq)cos
30°－μ(mg＋Eq)L＝mv－0，解得vC＝2 m/s.
(2)以小球为研究对象，在由C点至D点的运动过程中，
根据机械能守恒定律可得
mv＝mv＋mg·2R
在最高点以小球为研究对象，可得FN＋mg＝m，
解得FN＝30 N，vD＝2 m/s.
(3)设小球做类平抛运动的加速度大小为a，根据牛顿第二定律可得mg＋qE＝ma，解得a＝20 m/s2
假设小球落在BC段，则应用类平抛运动的规律列式可得x＝vDt,2R＝at2，
解得x＝ m＜ m，假设正确．
(责任编辑：admin)