⊳思维建模能力的培养

⊳规范表达能力的培养

1．在应用机械能守恒定律处理实际问题时，经常遇到像“链条”“液柱”类的物体，其在运动过程中将发生形变，其重心位置相对物体也发生变化，因此这类物体不能再看作质点来处理．

2．一般情况下，可将物体分段处理，确定质量分布均匀的规则物体各部分的重心位置，根据初、末状态物体重力势能的变化列式求解．

例1　如图1所示，一条长为L的柔软匀质链条，开始时静止在光滑梯形平台上，斜面上的链条长为x₀，已知重力加速度为g，L<BC，∠BCE＝α，试用x₀、x、L、g、α表示斜面上链条长为x时链条的速度大小(链条尚有一部分在平台上且x>x₀)．

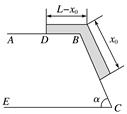
图1

答案　

解析　链条各部分和地球组成的系统机械能守恒，设链条的总质量为m，以平台所在位置为零势能面，当斜面上链条长为x时，有

－x₀g·x₀sin α＝mv²－xg·xsin α

解得v＝.

1．利用等效法计算势能变化时一定要注意等效部分的质量关系，即根据物体的相对位置关系将物体分成若干段，在应用相关规律求解时要注意对应各部分的质量关系．

2．解决涉及重力势能变化的问题时，物体的位置变化要以重心位置变化为准．

规范答题要求：适当的文字叙述，突出关键公式，公式符号与题目对应，说明假设的未知量符号．

例2　(13分)如图2所示，质量m＝2 kg的小球以初速度v₀沿光滑的水平面飞出后，恰好无碰撞地从A点进入竖直平面内的光滑圆弧轨道，其中B点为圆弧轨道的最低点，C点为圆弧轨道的最高点，圆弧AB对应的圆心角θ＝53°，圆半径R＝0.5 m．若小球离开水平面运动到A点所用时间t＝0.4 s，求：(sin 53°＝0.8，cos 53°＝0.6，g＝10 m/s²)

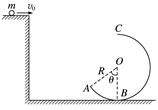
图2

(1)小球沿水平面飞出的初速度v₀的大小．

(2)到达B点时，小球对圆弧轨道的压力大小．

(3)小球能否通过圆弧轨道的最高点C？说明原因．

答案　(1)3 m/s　(2)136 N　(3)见解析

【书面表达过程】　(1)小球离开水平面运动到A点的过程中做平抛运动，有v_y＝gt(1分)

根据几何关系可得tan θ＝(1分)

代入数据，解得v₀＝3 m/s(1分)

(2)由题意可知，小球在A点的速度v_A＝(1分)

小球从A点运动到B点的过程，满足机械能守恒定律，有

mv＋mgR(1－cos θ)＝mv(2分)

设小球运动到B点时受到圆弧轨道的支持力为F_N，根据牛顿第二定律有

F_N－mg＝m(1分)

代入数据，解得F_N＝136 N(1分)

由牛顿第三定律可知，小球对圆弧轨道的压力大小为

F_N′＝F_N＝136 N(1分)

(3)假设小球能通过最高点C，则小球从B点运动到C点的过程满足机械能守恒定律，有

mv＝mg·2R＋mv(2分)

在C点有F_向＝m(1分)

代入数据，解得F_向＝36 N>mg(1分)

所以小球能通过最高点C.