第2讲 平抛运动
一、平抛运动 1.定义:以一定的初速度沿水平方向抛出的物体只在重力作用下的运动. 2.性质:平抛运动是加速度为g的匀加速曲线运动,其运动轨迹是抛物线. 3.平抛运动的条件 (1)v0≠0,沿水平方向;(2)只受重力作用. 4.研究方法 平抛运动可以分解为水平方向的匀速直线运动和竖直方向的匀变速直线运动. 5.基本规律(如图1所示)
图1
答案 运动时间t=,取决于高度h和当地的重力加速度g.水平射程x=v0t=v0,取决于初速度v0、高度h和当地的重力加速度g.当高度、重力加速度一定时,初速度越大,水平射程越大. 二、斜抛运动(说明:斜抛运动只作定性要求) 1.定义 将物体以初速度v0沿斜向上方或斜向下方抛出,物体只在重力作用下的运动. 2.性质 加速度为重力加速度g的匀变速曲线运动,轨迹是抛物线. 3.研究方法 斜抛运动可以看做水平方向的匀速直线运动和竖直方向的匀变速直线运动的合运动.
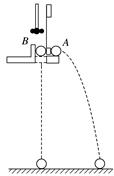
1.判断下列说法是否正确. (1)平抛运动的轨迹是抛物线,速度方向时刻变化,加速度方向也可能时刻变化.(×) (2)无论初速度是斜向上方还是斜向下方的斜抛运动都是匀变速曲线运动.(√) (3)做平抛运动的物体质量越大,水平位移越大.(×) (4)做平抛运动的物体初速度越大,落地时竖直方向的速度越大.(×) (5)从同一高度水平抛出的物体,不计空气阻力,初速度大的落地速度大.(√) 2.(人教版必修2P10做一做改编)(多选)为了验证平抛运动的小球在竖直方向上做自由落体运动,用如图2所示的装置进行实验.小锤打击弹性金属片后,A球水平抛出,同时B球被松开,自由下落,关于该实验,下列说法中正确的有( )
图2 A.两球的质量应相等 B.两球应同时落地 C.应改变装置的高度,多次实验 D.实验也能说明A球在水平方向上做匀速直线运动 答案 BC 解析 小锤打击弹性金属片后,A球做平抛运动,B球做自由落体运动.A球在竖直方向上的运动情况与B球相 同,做自由落体运动,因此两球同时落地.实验时,需A、B两球从同一高度开始运动,对质量没有要求,但两球的初始高度及击打力度应该有变化,实验时要进行3~5次得出结论.本实验不能说明A球在水平方向上的运动性质,故选项B、C正确,选项A、D错误. 3.(教科版必修2P18第2题)一架投放救援物资的飞机在某个受援区域的上空水平地匀速飞行,从飞机上每隔1 s投下1包救援物资,先后共投下4包,若不计空气阻力,则4包物资落地前( ) A.在空中任何时刻总是排成抛物线,它们的落地点是等间距的 B.在空中任何时刻总是排成抛物线,它们的落地点不是等间距的 C.在空中任何时刻总在飞机正下方排成竖直的直线,它们的落地点是等间距的 D.在空中任何时刻总在飞机正下方排成竖直的直线,它们的落地点不是等间距的 答案 C 4.如图3所示,在水平路面上一运动员驾驶摩托车跨越壕沟,壕沟两侧的高度差为0.8 m,水平距离为8 m,则运动员跨过壕沟的初速度至少为(g取10 m/s2)( )
图3 A.0.5 m/s B.2 m/s C.10 m/s D.20 m/s 答案 D
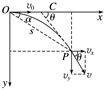
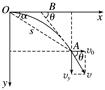
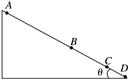
命题点一 平抛运动的基本规律 1.飞行时间:由t=知,时间取决于下落高度h和当地的重力加速度g,与初速度v0无关. 2.水平射程:x=v0t=v0,即水平射程由初速度v0、下落高度h和当地的重力加速度g共同决定,与其他因素无关. 3.落地速度:v==,以θ表示落地速度与x轴正方向间的夹角,有tan θ==,所以落地速度只与初速度v0、下落高度h以及当地重力加速度g有关. 4.两个重要推论 (1)做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图4所示,即xB=. 推导: ⇒xB= (2)做平抛(或类平抛)运动的物体在任一时刻,设其速度方向与水平方向的夹角为θ,位移方向与水平方向的夹角为α,则tan θ=2tan α.如图4所示. 推导:
图4 ⇒tan θ=2tan α
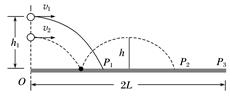
图5 A.A、B的运动时间相同 B.A、B沿x轴方向的位移相同 C.A、B运动过程中的加速度大小相同 D.A、B落地时速度大小相同
答案 D 解析 设O点与水平面的高度差为h,由h=gt,=gsin θ·t可得:t1=,t2= ,故t1<t2,A错误;由x1=v0t1,x2=v0t2,可知,x1<x2,B错误;由a1=g,a2=gsin θ可知,C错误;A落地的速度大小为vA==,B落地的速度大小vB==,所以vA=vB,故D正确.
1.(2015·浙江理综·17)如图6所示为足球球门,球门宽为L.一个球员在球门中心正前方距离球门s处高高跃起,将足球顶入球门的左下方死角(图中P点).球员顶球点的高度为h,足球做平抛运动(足球可看成质点,忽略空气阻力),则( )
图6 A.足球位移的大小x= B.足球初速度的大小v0= C.足球末速度的大小v= D.足球初速度的方向与球门线夹角的正切值tan θ= 答案 B 解析 足球位移大小为x==,A错误;根据平抛运动规律有:h=gt2,=v0t,解得v0= ,B正确;根据动能定理mgh=mv2-mv可得v==,C错误;足球初速度方向与球门线夹角正切值tan θ==,D错误. 2.(多选)在如图7所示的平面直角坐标系中,A、B、C三个小球沿图示方向做平抛运动,下列表述正确的是( )
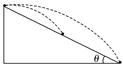
图7 A.若A、B、C同时抛出,恰好能在地面相遇,需要满足vC>vB>vA B.若A、B能在地面相遇,则A、B在空中运动的时间之比为2∶1 C.若A、C在(x0,0)相遇,则一定满足vA=vC D.只要B、C同时开始做平抛运动,二者绝不可能在空中相遇 答案 CD 命题点二 与斜面有关的平抛运动问题 1.从斜面上平抛(如图8)
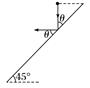
图8 已知位移方向,方法:分解位移 x=v0t y=gt2 tan θ= 可求得t= 2.对着斜面平抛(如图9) 已知速度的大小或方向,方法:分解速度
图9 vx=v0 vy=gt tan θ== 可求得t=
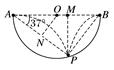
图10 (1)A点与O点的距离L; (2)运动员离开O点时的速度大小; (3)运动员从O点飞出开始到离斜坡距离最远所用的时间.
答案 (1)75 m (2)20 m/s (3)1.5 s 解析 (1)运动员在竖直方向做自由落体运动,有 Lsin 37°=gt2, L==75 m. (2)设运动员离开O点时的速度为v0,运动员在水平方向的分运动为匀速直线运动,有Lcos 37°=v0t, 即v0==20 m/s. (3)解法一 运动员的平抛运动可分解为沿斜面方向的匀加速运动(初速度为v0cos 37°、加速度为gsin 37°)和垂直斜面方向的类竖直上抛运动(初速度为v0sin 37°、加速度为gcos 37°). 当垂直斜面方向的速度减为零时,运动员离斜坡最远,有v0sin 37°=gcos 37°·t,解得t=1.5 s 解法二 当运动员的速度方向平行于斜坡或与水平方向成37°角时,运动员离斜坡最远,有=tan 37°,t=1.5 s.
平抛运动的分解方法与技巧 1.如果知道速度的大小或方向,应首先考虑分解速度. 2.如果知道位移的大小或方向,应首先考虑分解位移. 3.两种分解方法 (1)沿水平方向的匀速运动和竖直方向的自由落体运动; (2)沿斜面方向的匀加速运动和垂直斜面方向的匀减速运动.
3.如图11所示,小球以v0正对倾角为θ的斜面水平抛出,若小球到达斜面的位移最小,则飞行时间t为(重力加速度为g)( )
图11 A.v0tan θ B. C. D. 答案 D 解析 如图所示,要使小球到达斜面的位移最小,则小球落点与抛出点的连线应与斜面垂直,所以有tan θ=,而x=v0t,y=gt2,解得t=.
4.(多选)如图12所示,倾角为θ的斜面上有A、B、C三点,现从这三点分别以不同的初速度水平抛出一小球,三个小球均落在斜面上的D点,今测得AB∶BC∶CD=5∶3∶1,由此可判断( )
图12 A.A、B、C处三个小球运动时间之比为1∶2∶3 B.A、B、C处三个小球落在斜面上时速度与初速度间的夹角之比为1∶1∶1 C.A、B、C处三个小球的初速度大小之比为3∶2∶1 D.A、B、C处三个小球的运动轨迹可能在空中相交 答案 BC 解析 由于沿斜面AB∶BC∶CD=5∶3∶1,故三个小球在竖直方向运动的位移之比为9∶4∶1,运动时间之比为3∶2∶1,A项错误;斜面上平抛的小球落在斜面上时,速度与初速度之间的夹角α满足tan α=2tan θ,与小球抛出时的初速度大小和位置无关,因此B项正确;同时tan α=,所以三个小球的初速度之比等于运动时间之比,为3∶2∶1,C项正确;三个小球的运动轨迹(抛物线)在D点相交,因此不会在空中相交,D项错误. 命题点3 平抛运动中的临界问题
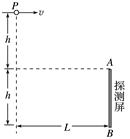
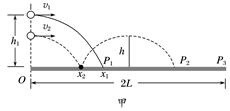
图13 (1)若微粒打在探测屏AB的中点,求微粒在空中飞行的时间; (2)求能被屏探测到的微粒的初速度范围.
答案 (1) (2)≤v≤L 解析 (1)打在AB中点的微粒,则h=gt2 解得t= (2)设打在B点的微粒初速度为v1,则 v1=,2h=gt 解得v1= 同理,设打在A点的微粒初速度为v2,则v2=L 所以微粒初速度范围为≤v≤L.
极限分析法在临界问题中的应用 分析平抛运动中的临界问题时一般运用极限分析的方法,即把要求的物理量设定为极大或极小,让临界问题突显出来,找到产生临界的条件.
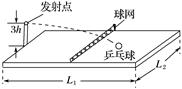
5.一带有乒乓球发射机的乒乓球台如图14所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h.不计空气的作用,重力加速度大小为g.若乒乓球的发射速率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,则v的最大取值范围是( )
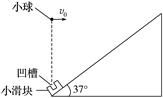
图14 A.<v<L1 B.<v< C.<v< D.<v< 答案 D 解析 发射机无论向哪个方向水平发射,乒乓球都做平抛运动.当速度v最小时,球沿中线恰好过网,有: 3h-h=① =v1t1② 联立①②两式,得v1= 当速度v最大时,球斜向右侧台面两个角发射,有 =v2t2③ 3h=gt④ 联立③④两式,得v2= 所以使乒乓球落到球网右侧台面上,v的最大取值范围为<v< ,选项D正确. 6.如图15所示,倾角为37°的粗糙斜面的底端有一质量m=1 kg的凹形小滑块,小滑块与斜面间的动摩擦因数μ=0.25.现小滑块以某一初速度v从斜面底端上滑,同时在斜面底端正上方有一小球以v0水平抛出,经过0.4 s,小球恰好垂直斜面方向落入凹槽,此时,小滑块还在上滑过程中.已知sin 37°=0.6,cos 37°=0.8,g取10 m/s2.求:
图15 (1)小球水平抛出的速度大小v0; (2)小滑块的初速度大小v. 答案 (1)3 m/s (2)5.35 m/s 解析 (1)设小球落入凹槽时竖直速度为vy,则 vy=gt=10×0.4 m/s=4 m/s v0=vytan 37°=3 m/s (2)小球落入凹槽时的水平位移x=v0t=3×0.4 m=1.2 m 则滑块的位移为x′= m=1.5 m 滑块上滑时,mgsin 37°+μmgcos 37°=ma 解得a=8 m/s2 根据公式x′=vt-at2 解得:v=5.35 m/s.
处理平抛运动的临界和极值问题的两种妙法 一、极端分析法 所谓极端分析法,是指两个变量之间的关系,若是单调上升或单调下降的函数关系,可以通过连续地改变某个变量甚至达到变化的极端,来对另一个变量进行判断的研究方法.
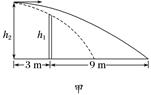
图16 (1)设击球点在3 m线正上方高度为2.5 m处,试问击球的速度在什么范围内才能使球既不触网也不越界? (2)若击球点在3 m线正上方的高度小于某个值,那么无论击球的速度多大,球不是触网就是越界,试求这个高度. 答案 见解析 解析 (1)如图甲所示,设球刚好擦网而过,则击球点到擦网点的水平位移x1=3 m,竖直位移y1=h2-h1=(2.5-2) m=0.5 m,根据位移关系x=vt,y=gt2,可得v=x ,代入数据可得v1=3 m/s,即所求击球速度的下限
设球刚好打在边界线上,则击球点到落地点的水平位移x2=12 m,竖直位移y2=h2=2.5 m,代入上面的速度公式v=x ,可求得v2=12 m/s,即所求击球速度的上限 欲使球既不触网也不越界,则击球速度v应满足3 m/s<v<12 m/s. (2)设击球点高度为h3时,球恰好既触网又压线,如图乙所示
设此时排球的初速度为v,击球点到触网点的水平位移x3=3 m,竖直位移y3=h3-h1=(h3-2) m,代入速度公式v=x 可得v=3 ;同理对压线点有x4=12 m,y4=h3,代入速度公式v=x 可得v=12 两式联立解得h3≈2.13 m,即当击球高度小于2.13 m时,无论球被水平击出的速度多大,球不是触网,就是越界. 二、对称法 所谓对称法,就是利用所给物理问题结构上的对称性或物理过程在时间、空间上的对称性,把已知结论推广,从而简化运算过程的处理方法.用对称法解题的关键是抓住事物在某一方面的对称性,这些对称性往往就是通往答案的捷径.一般情况下,对称性表现为研究对象在结构上的对称性、物理过程在时间上和空间上的对称性、物理量在分布上的对称性及作用效果的对称性等.
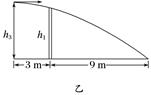
图17 (1)若球在球台边缘O点正上方高度为h1处以速度v1水平发出,落在球台上的P1点(如图17实线所示),求P1点距O点的距离x1. (2)若球从O点正上方以速度v2水平发出,恰好在最高点时越过球网落在球台上的P2点(如图虚线所示),求v2的大小. (3)若球从O点正上方水平发出后,球经反弹恰好越过球网且刚好落在对方球台边缘P3点,求发球点距O点的高度h3. 答案 (1)v1 (2) (3)h 解析 (1)如图甲所示,根据平抛规律得:
h1=gt,x1=v1t1 联立解得:x1=v1 . (2)根据平抛规律得:h2=gt,x2=v2t2 且h2=h,2x2=L,联立解得v2= . (3)如图乙所示,得:h3=gt,x3=v3t3
且3x3=2L 设球从恰好越过球网到达到最高点时所用的时间为t,水平距离为s,有h3-h=gt2,s=v3t 由几何关系得:x3+s=L 解得:h3=h.
题组1 平抛运动基本规律的应用 1.(多选)2015年国际乒联世界巡回赛瑞典公开赛落下战幕,中国乒乓球队包揽男女单打、男女双打四个冠军.在比赛中,乒乓球先后两次落台后恰好在等高处水平越过球网,过网时的速度方向均垂直于球网,把两次的乒乓球看成完全相同的两个球,球1和球2,如图1所示,不计乒乓球的旋转和空气阻力,乒乓球自起跳到最高点的过程中,下列说法中正确的是( )
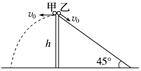
图1 A.起跳时,球1的重力功率等于球2的重力功率 B.球1的速度变化率小于球2的速度变化率 C.球1的飞行时间大于球2的飞行时间 D.过网时球1的速度大于球2的速度 答案 AD 解析 乒乓球起跳后到最高点的过程,其逆过程可看成平抛运动.重力的瞬时功率等于重力乘以竖直方向的速度,两球起跳后能到达的最大高度相同,由v2=2gh得起跳时竖直方向分速度大小相等,所以两球起跳时重力功率大小相等,A正确.速度变化率即加速度,两球在空中的加速度都等于重力加速度,所以两球的速度变化率相同,B错误.由h=gt2可得两球飞行时间相同,C错误.由x=vt可知,球1的水平位移较大,运动时间相同,则球1的水平速度较大,D正确. 2.如图2所示,离地面高h处有甲、乙两个小球,甲以初速度v0水平射出,同时乙以大小相同的初速度v0沿倾角为45°的光滑斜面滑下,若甲、乙同时到达地面,则v0的大小是( )
图2 A. B. C. D.2 答案 A 解析 甲球做平抛运动,由h=gt2,解得飞行时间t1=.乙球下滑加速度a=gsin 45°=g.由匀变速直线运动规律得h=v0t2+at,根据题述,甲、乙同时到达地面,t1=t2,联立解得v0=,选项A正确. 3.(多选)如图3所示为竖直截面为半圆形的容器,O为圆心,且AB为沿水平方向的直径.一物体在A点以向右的水平初速度vA抛出,与此同时另一物体在B点以向左的水平初速度vB抛出,两物体都落到容器的同一点P.已知∠BAP=37°,下列说法正确的是( )
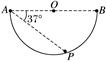
图3 A.B比A先到达P点 B.两物体一定同时到达P点 C.抛出时,两物体的速度大小之比为vA∶vB=16∶9 D.抛出时,两物体的速度大小之比为vA∶vB=32∶8 答案 BC 解析 两物体同时抛出,都落到P点,由平抛运动规律可知两物体下落了相同的竖直高度,由H=,得t= ,同时到达P点,A错误,B正确.在水平方向,抛出的水平距离之比等于抛出速度之比,设圆的半径为R,由几何关系得xAM=2Rcos2 37°,而xBM=xMPtan 37°,xMP=xAPsin 37°,xAP=2Rcos 37°,联立上述表达式得xAM∶xBM=16∶9,C正确,D错误.
4.如图4所示,一长为L的木板,倾斜放置,倾角为45°,今有一弹性小球,从与木板上端等高的某处自由释放,小球落到木板上反弹时,速度大小不变,碰撞前后,速度方向与木板夹角相等,欲使小球一次碰撞后恰好落到木板下端,则小球释放点距木板上端的水平距离为( )
图4 A.L B.L C.L D.L 答案 D 解析 设小球释放点距木板上端的水平距离为x,由θ=45°可知,小球自由下落高度h=x,由v=2gh可得:v0=. 水平抛出后,小球落到木板下端时竖直方向速度vy=,由竖直位移和水平位移相等可得:vyt=v0t,解得:x=,故D正确. 题组2 与斜面有关的平抛运动问题 5.(多选)如图5所示,在斜面顶端先后水平抛出同一小球,第一次小球落到斜面中点,第二次小球落到斜面底端,从抛出到落至斜面上(忽略空气阻力)( )
图5 A.两次小球运动时间之比t1∶t2=1∶ B.两次小球运动时间之比t1∶t2=1∶2 C.两次小球抛出时初速度之比v01∶v02=1∶ D.两次小球抛出时初速度之比v01∶v02=1∶2 答案 AC 解析 两次小球在竖直方向上均做自由落体运动,两次小球下落高度之比为1∶2,由自由落体运动规律可知,运动时间之比为1∶,选项A正确,B错误;水平方向两次小球均做匀速直线运动,由水平位移关系以及时间关系可得初速度之比为1∶,选项C正确,D错误. 6.如图6所示为湖边一倾角为30°的大坝的横截面示意图,水面与大坝的交点为O.一人站在A点处以速度v0沿水平方向扔小石块,已知AO=40 m,g取10 m/s2.下列说法正确的是( )
图6 A.若石块不能落入水中,则v0越大,落到斜面上时速度方向与斜面的夹角越大 B.若石块不能落入水中,则v0越大,落到斜面上时速度方向与斜面的夹角越小 C.若石块能落入水中,则v0越大,落水时速度方向与水平面的夹角越大 D.若v0=18 m/s,则石块可以落入水中 答案 D 解析 若石块不能落入水中,速度方向与水平方向的夹角的正切值tan α=,位移方向与水平方向夹角的正切值tan θ==,可知tan α=2tan θ,因为θ一定,则速度与水平方向的夹角一定,可知石块落到斜面上时速度方向与斜面的夹角一定,与初速度无关,故A、B错误.若石块能落入水中,则落水时下落的高度一定,可知竖直分速度一定,根据tan α=知,初速度越大,则落水时速度方向与水平面的夹角越小,故C错误.根据h=得t=2 s,则石块落入水中的最小初速度vmin=10 m/s<18 m/s, 故D正确. 7.(多选)如图7所示,光滑斜面固定在水平面上,顶端O有一小球,从静止释放,运动到底端B的时间为t1,若给小球不同的水平初速度,落到斜面上的A点,经过的时间为t2,落到斜面底端B点,经过的时间为t3,落到水平面上的C点,经过的时间为t4,则( )
图7 A.t2>t1 B.t3>t2 C.t4>t3 D.t1>t4 答案 BD 解析 由=gsin α·t可得t1= ,而t4=t3=,故有C错误,D正确;由t2<可得:t1>t2,t3>t2,A错误,B正确. 8.如图8所示,滑板运动员从倾角为53°的斜坡顶端滑下,滑下的过程中他突然发现在斜面底端有一个高h=1.4 m、宽L=1.2 m的长方体障碍物,为了不触及这个障碍物,他必须在距水平地面高度H=3.2 m的A点沿水平方向跳起离开斜面(竖直方向的速度变为0).已知运动员的滑板与斜面间的动摩擦因数μ=0.1,忽略空气阻力,重力加速度g取10 m/s2.(已知sin 53°=0.8,cos 53°=0.6)求:
图8 (1)运动员在斜面上滑行的加速度的大小; (2)若运动员不触及障碍物,他从斜面上起跳后到落至水平面的过程所经历的时间; (3)运动员为了不触及障碍物,他从A点沿水平方向起跳的最小速度. 答案 (1)7.4 m/s2 (2)0.8 s (3)6.0 m/s 解析 (1)设运动员连同滑板的质量为m,运动员在斜面上滑行的过程中,根据牛顿第二定律有 mgsin 53°-μmgcos 53°=ma, 解得运动员在斜面上滑行的加速度a=7.4 m/s2. (2)运动员从斜面上起跳后沿竖直方向做自由落体运动, 根据自由落体运动规律有H=gt2,解得t=0.8 s. (3)为了不触及障碍物,运动员以速度v沿水平方向起跳后竖直下落高度为H-h时,他沿水平方向运动的距离为+L,设该段时间为t′,则H-h=gt′2,+L=vt′, 解得v=6.0 m/s. 题组3 平抛运动中的临界问题 9.如图9所示, 可视为质点的小球,位于半径为 m半圆柱体左端点A的正上方某处,以一定的初速度水平抛出小球,其运动轨迹恰好能与半圆柱体相切于B点.过B点的半圆柱体半径与水平方向的夹角为60°,则初速度为(不计空气阻力,重力加速度g取10 m/s2)( )
图9 A. m/s B.4 m/s C.3 m/s D. m/s 答案 C 解析 小球飞行过程中恰好与半圆柱体相切于B点,可知在B点的速度与水平方向的夹角为30°,设位移与水平方向的夹角为θ,则有tan θ==.因为tan θ==,则竖直位移为y=R,v=2gy=gR,又有tan 30°=,联立以上各式解得v0= = m/s=3 m/s,故选C. 10.如图10所示,水平屋顶高H=5 m,围墙高h=3.2 m,围墙到房子的水平距离L=3 m,围墙外空地宽x=10 m,为使小球从屋顶水平飞出落在围墙外的空地上,g取10 m/s2.求:
图10 (1)小球离开屋顶时的速度v0的大小范围; (2)小球落在空地上的最小速度. 答案 (1)5 m/s≤v0≤13 m/s (2)5 m/s 解析 (1)设小球恰好落到空地的右侧边缘时的水平初速度为v01,则小球的水平位移:L+x=v01t1 小球的竖直位移:H=gt 联立两式得v01=(L+x) =13 m/s 设小球恰好越过围墙的边缘时的水平初速度为v02,则此过程中小球的水平位移:L=v02t2 小球的竖直位移:H-h=gt 联立两式得:v02=L=5 m/s 小球离开屋顶时的速度大小为5 m/s≤v0≤13 m/s (2)小球落在空地上,下落高度一定,落地时的竖直分速度一定,当小球恰好越过围墙的边缘落在空地上时,落地速度最小. 竖直方向:v=2gH 又有:vmin= 代入数据解得:vmin=5 m/s
|
|||||||||||||||||||