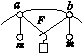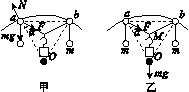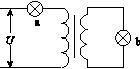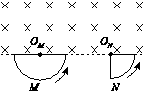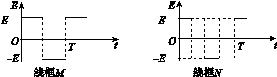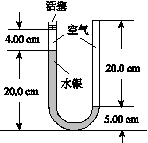|
2016·全国卷Ⅲ(物理)
14.D5[2016·全国卷Ⅲ] 关于行星运动的规律,下列说法符合史实的是( ) A.开普勒在牛顿定律的基础上,导出了行星运动的规律 B.开普勒在天文观测数据的基础上,总结出了行星运动的规律 C.开普勒总结出了行星运动的规律,找出了行星按照这些规律运动的原因 D.开普勒总结出了行星运动的规律,发现了万有引力定律 14.B [解析] 开普勒在天文观测数据的基础上,总结出了行星运动的规律,牛顿在开普勒研究基础上结合自己发现的牛顿运动定律,发现了万有引力定律,指出了行星按照这些规律运动的原因,选项B正确. 15.I2[2016·全国卷Ⅲ] 关于静电场的等势面,下列说法正确的是( ) A.两个电势不同的等势面可能相交 B.电场线与等势面处处相互垂直 C.同一等势面上各点电场强度一定相等 D.将一负的试探电荷从电势较高的等势面移至电势较低的等势面,电场力做正功 15.B [解析] 静电场中的电场线不可能相交,等势面也不可能相交,否则的话会出现一个点有两个电场强度和两个电势值的矛盾,A错误;由WAB=qUAB可知,当电荷在等势面上移动时,电荷的电势能不变,如果电场线不与等势面垂直,那么电荷将受到电场力,在电荷运动时必然会做功并引起电势能变化,这就矛盾了,B正确;同一等势面上各点电势相等,但电场强度不一定相等,C错误;对于负电荷,q<0,从电势高的A点移到电势低的B点,UAB>0,由电场力做功的公式WAB=qUAB可知WAB<0,电场力做负功,D错误. 16.A2 E2[2016·全国卷Ⅲ] 一质点做速度逐渐增大的匀加速直线运动,在时间间隔t内位移为s,动能变为原来的9倍.该质点的加速度为( ) A. B. C. D. 16.A [解析] 由Ek=mv2可知速度变为原来的3倍.设加速度为a,初速度为v,则末速度为3v.由速度公式vt=v0+at得3v=v+at,解得at=2v;由位移公式s=v0t+at2得s=vt+·at·t=vt+·2v·t=2vt,进一步求得v=;所以a==·=,A正确. 17.B4[2016·全国卷Ⅲ] 如图1所示,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )
图1 A. B.m C.m D.2m 17.C [解析] 对a受力分析如图甲所示,其中虚线三角形为等边三角形,由正交分解法可得Fsin α=mgsin 30°,又知F=mg,故α=30°;对小物块的悬挂点受力分析如图乙所示,由力的合成可得2Fcos(α+30°)=Mg,故可得M=m,C正确.
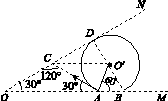
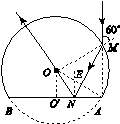
18.K2[2016·全国卷Ⅲ] 平面OM和平面ON之间的夹角为30°,其横截面(纸面)如图1所示,平面OM上方存在匀强磁场,磁感应强度大小为B,方向垂直于纸面向外.一带电粒子的质量为m,电荷量为q(q>0).粒子沿纸面以大小为v的速度从OM的某点向左上方射入磁场,速度与OM成30°角.已知该粒子在磁场中的运动轨迹与ON只有一个交点,并从OM上另一点射出磁场.不计重力.粒子离开磁场的出射点到两平面交线O的距离为( )
图1 A. B. C. D. 18.D [解析] 设射入磁场的入射点为A,延长入射速度v所在直线交ON于一点C,则轨迹圆与AC相切;由于轨迹圆只与ON有一个交点,所以轨迹圆与ON相切,所以轨迹圆的圆心必在∠ACD的角平分线上,作出轨迹圆如图所示,其中O′为圆心,B为出射点.
由几何关系可知∠O′CD=30°,Rt△O′DC中,CD=O′D·cot 30°=R;由对称性知,AC=CD=R;等腰△ACO中,OA=2AC·cos 30°=3R;等边△O′AB中,AB=R,所以OB=OA+AB=4R.由qvB=m得R=,所以OB=,D正确. 19.M2[2016·全国卷Ⅲ] 如图1所示,理想变压器原、副线圈分别接有额定电压相同的灯泡a和b.当输入电压U为灯泡额定电压的10倍时,两灯泡均能正常发光.下列说法正确的是( )
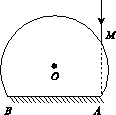
图1 A.原、副线圈匝数比为9∶1 B.原、副线圈匝数比为1∶9 C.此时a和b的电功率之比为9∶1 D.此时a和b的电功率之比为1∶9 19.AD [解析] 设灯泡的额定电压为U0,则输入电压U=10U0,由于两灯泡均正常发光,故原线圈两端的电压U1=U-U0=9U0,副线圈两端的电压U2=U0,所以原、副线圈的匝数比n1∶n2=U1∶U2=9∶1,A正确,B错误;原、副线圈的电流之比I1∶I2=n2∶n1=1∶9,由电功率P=UI可知,a和b的电功率之比为1∶9,C错误,D正确. 20.D4 E2[2016·全国卷Ⅲ] 如图所示,一固定容器的内壁是半径为R的半球面;在半球面水平直径的一端有一质量为m的质点P.它在容器内壁由静止下滑到最低点的过程中,克服摩擦力做的功为W.重力加速度大小为g.设质点P在最低点时,向心加速度的大小为a,容器对它的支持力大小为N,则( )
图1 A.a= B.a= C.N= D.N= 20.AC [解析] 质点P下滑到底端的过程,由动能定理得mgR-W=mv2-0,可得v2=,所以a==,A正确,B错误;在最低点,由牛顿第二定律得N-mg=m,故N=mg+m=mg+·=,C正确,D错误. 21.L2 M1[2016·全国卷Ⅲ] 如图所示,M为半圆形导线框,圆心为OM;N是圆心角为直角的扇形导线框,圆心为ON;两导线框在同一竖直面(纸面)内;两圆弧半径相等;过直线OMON的水平面上方有一匀强磁场,磁场方向垂直于纸面.现使线框M、N在t=0时从图示位置开始,分别绕垂直于纸面、且过OM和ON的轴,以相同的周期T逆时针匀速转动,则( )
图1 A.两导线框中均会产生正弦交流电 B.两导线框中感应电流的周期都等于T C.在t=时,两导线框中产生的感应电动势相等 D.两导线框的电阻相等时,两导线框中感应电流的有效值也相等 21.BC [解析] 设导线圈半径为l,角速度为ω,两导线框切割磁感线的等效长度始终等于圆弧半径,因此在产生感应电动势时其瞬时感应电动势大小始终为E=Bωl2,但进磁场和出磁场时电流方向相反,所以线框中应该产生方波交流式电,如图所示,A错误;由T=可知,两导线框中感应电流的周期相同,均为T,B正确;在t=时,两导线框均在切割磁感线,故两导线框中产生的感应电动势均为Bωl2,C正确;对于线框M,有·+·=·T,解得U有M=E;对于线框N,有·+0+·+0=·T,解得U有N=E,故两导线框中感应电流的有效值并不相等,D错误.
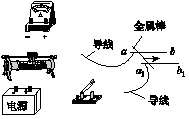
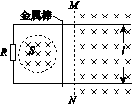
22.J10 K1[2016·全国卷Ⅲ] 某同学用图1中所给器材进行与安培力有关的实验.两根金属导轨ab和a1b1固定在同一水平面内且相互平行,足够大的电磁铁(未画出)的N极位于两导轨的正上方,S极位于两导轨的正下方,一金属棒置于导轨上且与两导轨垂直.
图1 (1)在图中画出连线,完成实验电路.要求滑动变阻器以限流方式接入电路,且在开关闭合后,金属棒沿箭头所示的方向移动. (2)为使金属棒在离开导轨时具有更大的速度,有人提出以下建议: A.适当增加两导轨间的距离 B.换一根更长的金属棒 C.适当增大金属棒中的电流 其中正确的是________(填入正确选项前的标号). 22.[答案] (1)连线如图所示
(2)AC [解析] (1)限流式接法要求滑动变阻器接线时只能连接“一上一下”两个接线柱;磁铁N极位于上方,说明磁感线向下;开关闭合后,金属棒往右运动,说明棒受到向右的安培力;由左手定则可知,电流应垂直纸面向外(ab指向a1b1);所以应按“电源正极→开关→滑动变阻器下接线柱→滑动变阻器上接线柱→电流表→ab→a1b1→电源负极”的顺序连接回路. (2)由动能定理BIL·s=mv2-0可知,要增大金属棒离开导轨时的速度v,可以增大磁感应强度B、增大电流I、增大两导轨间的距离L或增大导轨的长度s;但两导轨间的距离不变而只是换一根更长的金属棒后,等效长度L并不会发生改变,但金属棒的质量增大,故金属棒离开导轨时的速度v减小. 23.C4C4[2016·全国卷Ⅲ] 某物理课外小组利用图(a)中的装置探究物体加速度与其所受合外力之间的关系.图中,置于实验台上的长木板水平放置,其右端固定一轻滑轮;轻绳跨过滑轮,一端与放在木板上的小滑车相连,另一端可悬挂钩码.本实验中可用的钩码共有N=5个,每个质量均为0.010 kg.实验步骤如下: (1)将5个钩码全部放入小车中,在长木板左下方垫上适当厚度的小物块,使小车(和钩码)可以在木板上匀速下滑.
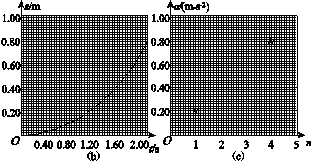
图1 (2)将n(依次取n=1,2,3,4,5)个钩码挂在轻绳右端,其余N-n个钩码仍留在小车内;用手按住小车并使轻绳与木板平行.释放小车,同时用传感器记录小车在时刻t相对于其起始位置的位移s,绘制s t图像,经数据处理后可得到相应的加速度a. (3)对应于不同的n的a值见下表.n=2时的s t图像如图(b)所示;由图(b)求出此时小车的加速度(保留2位有效数字),将结果填入下表.
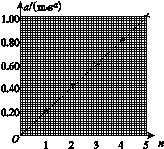
(4)利用表中的数据在图(c)中补齐数据点,并作出an图像.从图像可以看出:当物体质量一定时,物体的加速度与其所受的合外力成正比.
图1 (5)利用an图像求得小车(空载)的质量为______ kg(保留2位有效数字,重力加速度g取9.8 m/s2). (6)若以“保持木板水平”来代替步骤(1),下列说法正确的是 ________(填入正确选项前的标号). A.an图线不再是直线 B.an图线仍是直线,但该直线不过原点 C.an图线仍是直线,但该直线的斜率变大 23.[答案] (3)0.39(0.37~0.49均可) (4)an图线如图所示
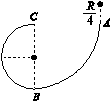
(5)0.45(0.43~0.47均可) (6)BC [解析] (3)系统做匀加速直线运动,s=at2,由图(b)可知,当t=2 s时,s=0.78 m,代入解得a=0.39 m/s2. (4)由题意知描点法作图所得的必须是一条直线. (5)对于挂在下面的n个钩码,有nmg-F=nma; 对于小车(含剩下的钩码),有F=[M+(N-n)m]a; 两式相加得nmg=(M+Nm)a; 解得a==n,可见an图像的斜率表示, 由an图可知斜率k=0.196,所以=0.196,解得M=0.45 kg. (6)木板水平时要考虑摩擦力的影响, 对于挂在下面的n个钩码,有nmg-F′=nma; 对于小车(含剩下的钩码),有F′-μ[M+(N-n)m]g=[M+(N-n)m]a; 两式相加得nmg-μ[M+(N-n)m]g=(M+Nm)a, 去中括号得n(mg+μmg)-μ(M+Nm)g=(M+Nm)a, 移项化简得n(mg+μmg)=(M+Nm)(a+μg), 解得a=·n-μg=·n-9.8μ, 可见an图像仍是一条直线,但其斜率要变大,且不过坐标原点. 24.C2 D4 E2[2016·全国卷Ⅲ] 如图1所示,在竖直平面内有由圆弧AB和圆弧BC组成的光滑固定轨道,两者在最低点B平滑连接.AB弧的半径为R,BC弧的半径为.一小球在A点正上方与A相距处由静止开始自由下落,经A点沿圆弧轨道运动. (1)求小球在B、A两点的动能之比; (2)通过计算判断小球能否沿轨道运动到C点.
图1 24.[答案] (1)5 (2)能 [解析] (1)设小球的质量为m,小球在A点的动能为EkA,由机械能守恒得EkA=mg ① 设小球在B点的动能为EkB,同理有EkB=mg ② 由①②式得=5 ③ (2)若小球能沿轨道运动到C点,小球在C点所受轨道的正压力N应满足N≥0 ④ 设小球在C点的速度大小为vC,由牛顿运动定律和向心加速度公式有N+mg= ⑤ 由④⑤式得,vC应满足mg≤m ⑥ 由机械能守恒有mg=mv ⑦ 由⑥⑦式可知,小球恰好可以沿轨道运动到C点. 25.L5[2016·全国卷Ⅲ] 如图1所示,两条相距l的光滑平行金属导轨位于同一水平面(纸面)内,其左端接一阻值为R的电阻;一与导轨垂直的金属棒置于两导轨上;在电阻、导轨和金属棒中间有一面积为S的区域,区域中存在垂直于纸面向里的均匀磁场,磁感应强度大小B1随时间t的变化关系为B1=kt,式中k为常量;在金属棒右侧还有一匀强磁场区域,区域左边界MN(虚线)与导轨垂直,磁场的磁感应强度大小为B0,方向也垂直于纸面向里.某时刻,金属棒在一外加水平恒力的作用下从静止开始向右运动,在t0时刻恰好以速度v0越过MN,此后向右做匀速运动.金属棒与导轨始终相互垂直并接触良好,它们的电阻均忽略不计.求: (1)在t=0到t=t0时间间隔内,流过电阻的电荷量的绝对值; (2)在时刻t(t>t0)穿过回路的总磁通量和金属棒所受外加水平恒力的大小.
图1 25.[答案] (1) (2)B0lv0(t-t0)+kSt (B0lv0+kS) [解析] (1)在金属棒未越过MN之前,t时刻穿过回路的磁通量为Φ=ktS ① 设在从t时刻到t+Δt的时间间隔内,回路磁通量的变化量为ΔΦ,流过电阻R的电荷量为Δq.由法拉第电磁感应定律有E= ② 由欧姆定律有i= ③ 由电流的定义有i= ④ 联立①②③④式得|Δq|=Δt ⑤ 由⑤式得,在t=0到t=t0的时间间隔内,流过电阻R的电荷量q的绝对值为 |q|= ⑥ (2)当t>t0时,金属棒已越过MN.由于金属棒在MN右侧做匀速运动,有f=F ⑦ 式中,f是外加水平恒力,F是匀强磁场施加的安培力.设此时回路中的电流为I,F的大小为 F=B0Il ⑧ 此时金属棒与MN之间的距离为s=v0(t-t0) ⑨ 匀强磁场穿过回路的磁通量为Φ′=B0ls ⑩ 回路的总磁通量为Φt=Φ+Φ′ 式中,Φ仍如①式所示.由①⑨⑩⑪式得,在时刻t(t>t0)穿过回路的总磁通量为 Φt=B0lv0(t-t0)+kSt ⑫ 在t到t+Δt的时间间隔内,总磁通量的改变ΔΦt为 ΔΦt=(B0lv0+kS)Δt ⑬ 由法拉第电磁感应定律得,回路感应电动势的大小为 Et= ⑭ 由欧姆定律有I= ⑮ 联立⑦⑧⑬⑭⑮式得f=(B0lv0+kS) ⑯ 33.H1 H2 H3[2016·全国卷Ⅲ] [物理——选修33] (1)关于气体的内能,下列说法正确的是________. A.质量和温度都相同的气体,内能一定相同 B.气体温度不变,整体运动速度越大,其内能越大 C.气体被压缩时,内能可能不变 D.一定量的某种理想气体的内能只与温度有关 E.一定量的某种理想气体在等压膨胀过程中,内能一定增加 (2)一U形玻璃管竖直放置,左端开口,右端封闭,左端上部有一光滑的轻活塞.初始时,管内汞柱及空气柱长度如图所示.用力向下缓慢推活塞,直至管内两边汞柱高度相等时为止.求此时右侧管内气体的压强和活塞向下移动的距离.已知玻璃管的横截面积处处相同;在活塞向下移动的过程中,没有发生气体泄漏;大气压强p0=75.0 cmHg.环境温度不变.
图1 33.[答案] (1)CDE (2)144 cmHg 9.42 cm [解析] (1)温度相同,分子平均动能相同,若摩尔质量不同,则相同质量的气体有不同的分子数,分子总动能不同,假若都是理想气体,因为只考虑分子动能,所以内能不同,A错误;气体内能取决于气体分子的平均动能和分子势能,而与宏观上整体的动能无关,B错误;若外界对气体做的功等于气体向外界放出的热,则气体的内能不变,C正确;理想气体的内能取决于气体分子的平均动能,而分子平均动能取决于温度,D正确;理想气体等压膨胀过程中,p一定,V增加,由=C可知T升高,故内能增加,E正确. (2)设初始时,右管中空气柱的压强为p1,长度为l1;左管中空气柱的压强为p2=p0,长度为l2.活塞被下推h后,右管中空气柱的压强为p′1,长度为l′1;左管中空气柱的压强为p′2,长度为l′2.以cmHg为压强单位.由题给条件得p1=p0+(20.0-5.00) cmHg ① l′1= cm ② 由玻意耳定律得 p1l1=p′1l′1 ③ 联立①②③式和题给条件得 p′1=144 cmHg ④ 依题意 p′2=p′1 ⑤ l′2=4.00 cm+ cm-h ⑥ 由玻意耳定律得 p2l2= p′2l′2 ⑦ 联立④⑤⑥⑦式和题给条件得 h=9.42 cm ⑧ 34.[2016·全国卷Ⅲ] [物理——选修34] G2(1)由波源S形成的简谐横波在均匀介质中向左、右传播.波源振动的频率为20 Hz,波速为16 m/s.已知介质中P、Q两质点位于波源S的两侧,且P、Q和S的平衡位置在一条直线上,P、Q的平衡位置到S的平衡位置之间的距离分别为15.8 m、14.6 m.P、Q开始振动后,下列判断正确的是________. A.P、Q两质点运动的方向始终相同 B.P、Q两质点运动的方向始终相反 C.当S恰好通过平衡位置时,P、Q两点也正好通过平衡位置 D.当S恰好通过平衡位置向上运动时,P在波峰 E.当S恰好通过平衡位置向下运动时,Q在波峰 N1(2)如图1所示,玻璃球冠的折射率为,其底面镀银,底面的半径是球半径的倍;在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的M点,该光线的延长线恰好过底面边缘上的A点.求该光线从球面射出的方向相对于其初始入射方向的偏角.
图1 34.[答案] (1)BDE (2)150° [解析] (1)波长λ=vT==0.8 m,SQ=14.6 m=18λ,当S处于平衡位置向上振动时,Q应处于波谷;SP=15.8 m=19λ,当S处于平衡位置向上振动时,P应处于波峰;可见P、Q两质点运动的方向应始终相反,A、C错误,B、D、E正确. (2)设球半径为R,球冠底面中心为O′,连接OO′,则OO′⊥AB.令∠OAO′=α,有 cos α== ① 即α=30° ②
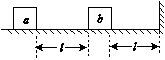
由题意MA⊥AB 所以∠OAM=60° 设图中N点为光线在球冠内底面上的反射点,所考虑的光线的光路图如图所示.设光线在M点的入射角为i、折射角为r,在N点的入射角为i′,反射角为i ″,玻璃折射率为n.由于△OAM为等边三角形,有 i=60° ④ 由折射定律有sin i=nsin r ⑤ 代入题给条件n=得r=30° ⑥ 作底面在N点的法线NE,由于NE∥AM,有i′=30° ⑦ 根据反射定律,有i ″=30° ⑧ 连接ON,由几何关系知△MAN≌△MON,故有∠MNO=60°⑨ 由⑦⑨式得∠ENO=30° ⑩ 于是∠ENO为反射角,ON为反射光线.这一反射光线经球面再次折射后不改变方向.所以,经一次反射后射出玻璃球冠的光线相对于入射光线的偏角β为 β=180°-∠ENO=150° ⑪ 35.[2016·全国卷Ⅲ] [物理——选修35] O2(1)一静止的铝原子核Al俘获一速度为1.0×107 m/s的质子p后,变为处于激发态的硅原子核Si*,下列说法正确的是________. A.核反应方程为p+Al―→Si* B.核反应过程中系统动量守恒 C.核反应过程中系统能量不守恒 D.核反应前后核子数相等,所以生成物的质量等于反应物的质量之和 E.硅原子核速度的数量级为105 m/s,方向与质子初速度的方向一致 F2 E6(2)如图1所示,水平地面上有两个静止的小物块a和b,其连线与墙垂直;a和b相距l,b与墙之间也相距l;a的质量为m,b的质量为m.两物块与地面间的动摩擦因数均相同,现使a以初速度v0向右滑动,此后a与b发生弹性碰撞,但b没有与墙发生碰撞.重力加速度大小为g.求物块与地面间的动摩擦因数满足的条件.
图1 35.[答案] (1)ABE (2)≤μ< [解析] (1)核反应方程为p+Al→Si*,A正确;核反应过程中系统动量守恒、能量守恒(只是前后表现形式不同罢了)、质量数守恒、电荷数守恒,但质量亏损,亏损部分以能量的形式释放出去,所以B正确,C、D错误;由动量守恒定律得0+m1v1=m2v2,即0+1×107=28v2,解得v2≈0.036×107 m/s=3.6×105 m/s,E正确. (2)设物块与地面间的动摩擦因数为μ.若要物块a、b能够发生碰撞,应有 mv>μmgl ① 即μ< ② 设在a、b发生弹性碰撞前的瞬间,a的速度大小为v1.由能量守恒有 mv=mv+μmgl ③ 设在a、b碰撞后的瞬间,a、b的速度大小分别为v′1、v′2,由动量守恒和能量守恒有 mv1=mv′1+v′2 ④ mv=mv′+v′ ⑤ 联立④⑤式解得v′2=v1 ⑥ 由题意,b没有与墙发生碰撞,由功能关系可知 v′≤μgl ⑦ 联立③⑥⑦式,可得 μ≥ ⑧ 联立②⑧式,a与b发生碰撞、但b没有与墙发生碰撞的条件 ≤μ< ⑨
|