学习物理网移动版

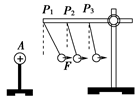
第九章 第2节　库仑定律

【学习目标】

1．通过库仑定律的探究过程，体会实验与类比在定律的建立过程中发挥的重要作用。

2． 通过与质点模型类比，知道点电荷模型的物理意义及建立点电荷模型的条件，进一步体会科学研究中的理想模型方法。

3．理解库仑定律的内涵和适用条件，能够应用库仑定律计算点电荷间的静电力，会利用力的合成的知识解决多个电荷间的相互作用问题。

4．体会库仑扭秤实验的设计思路与实验方法。

5． 对比库仑定律和万有引力定律的形式，体会物理学的和谐统一之美，提高物理学习兴趣。

【课前预习】

一、电荷之间的作用力

1．实验探究:

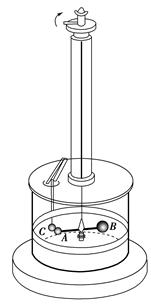
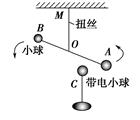
结论：电荷间的作用力随着电荷量的增加而增大，随着距离的增大而减小。

2．点电荷：是一种理想化模型。当带电体之间的距离较远时，对所研究问题没有影响，可以忽略带电体的形状、大小及电荷分布状况，而看作带电的点。

3．库仑定律：

(1)内容：真空中两个静止点电荷之间的相互作用力，与它们的电荷量的乘积成正比，与它们的距离的二次方成反比，作用力的方向在它们的连线上。

(2)表达式：F＝k，公式中k叫做静电力常量，k＝9.0×10⁹ N·m²/C²。

(3)定律的适用范围：①在真空中；②两个静止点电荷。(在空气中库仑定律也近似成立)

二、库仑的实验(了解)

1．实验装置

　

电荷分配规律：两个完全相同的导体球相互接触，若两导体球带同种电荷，会把总电荷量平分；若带异种电荷，则先中和然后再把剩余电荷量平分。

三、静电力计算

1．两个点电荷间的作用力用库仑定律计算；

2．两个或者两个以上点电荷对某一个点电荷的作用力等于各点电荷单独对这个点电荷的作用力的矢量和。(两个点电荷间的作用力不因第三个点电荷的存在而改变)

▲判一判

(1)实验表明电荷之间的作用力一定和电荷间的距离成反比。                (×)

(2)实验表明两个带电体的距离越大，作用力就越小。                            (√)

(3)点电荷是一个带有电荷的点，它是实际带电体的抽象，是一种理想化模型。   (√)

(4)球形带电体一定可以看成点电荷。                                                        (×)

(5)很大的带电体也有可能看作点电荷。                                                    (√)

 

 

【学习过程】

任务一：对点电荷的理解

[例1]下列关于点电荷的说法，正确的是(　　)

A．只有体积很小的带电体才能看成点电荷

B．体积很大的带电体一定不能看成点电荷

C．只有球形带电体才能看成点电荷

D．当两个带电体的大小远小于它们之间的距离时，可将这两个带电体看成点电荷

 

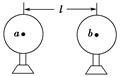
[变式训练1-1]美国东部一枚火箭从佛罗里达州肯尼迪航天中心39B发射塔冲天而起。这是美国未来载人航天工具——“战神Ⅰ－X”火箭的第一次升空。升空过程中由于与大气摩擦产生了大量的静电，如果这些静电没有被及时导走，下列情况中，升空后的“战神Ⅰ－X”火箭能被视为点电荷的是(　　)

A．研究“战神Ⅰ－X”火箭外部与其相距1 m处的一个带电微粒之间的静电力

B．研究“战神Ⅰ－X”火箭与地球(带负电)之间的静电力

C．任何情况下都可视为点电荷

D．任何情况下都不可视为点电荷

[变式训练1-2] (多选)下列关于点电荷的说法正确的是(　　)

A．两个带电体无论多大，只要它们之间的距离远大于它们的大小，这两个带电体就可以看作点电荷

B．一个带电体只要它的体积很小，则在任何情况下，都可以看作点电荷

C．一个体积很大的带电体，在任何情况下，都不能看作点电荷

D．两个带电的金属小球，不一定能将它们作为电荷集中在球心的点电荷处理

任务二：对库仑定律的理解

[例2]已知氢核(质子)的质量是1.67×10^－27 kg，电子的质量是9.1×10^－31 kg，在氢原子内它们之间的最短距离为5.3×10^－11 m．试比较氢原子核与电子之间的静电力和万有引力。

F_库＝k＝9.0×10⁹× N＝8.2×10^－8 N

F_引＝G＝6.7×10^－11× N＝3.6×10^－47 N

＝2.3×10³⁹

可知微观粒子间的万有引力远小于库仑力，因此在研究微观带电粒子的相互作用时，可以把万有引力忽略。

[变式训练2-1]如图所示，两个质量均为m的完全相同的金属球壳a与b，壳层的厚度和质量分布均匀，将它们分别固定于绝缘支座上，两球心间的距离为l，为球半径的3倍。若使它们带上等量异种电荷，两球电荷量的绝对值均为Q，那么a、b两球之间的万有引力F_引、库仑力F_库分别为(　　)

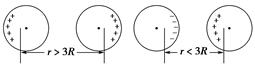
A．F_引＝G，F_库＝k  B．F_引≠G，F_库≠k

C．F_引≠G，F_库＝k  D．F_引＝G，F_库≠k

[变式训练2-2]两个分别带有电荷量－Q和＋3Q的相同金属小球(均可视为点电荷)，固定在相距为r的两处，它们间库仑力的大小为F。两小球相互接触后将其固定距离变为，则两球间库仑力的大小为(　　)

A．F　　　　B．F　　　C.F　　　D．12F

[变式训练2-3]两个半径均为R的带电金属球所带电荷量分别为Q₁和Q₂，当两球心相距3R时，相互作用的库仑力大小为(　　)

A．F＝k　　                              B．F＞k

C．F＜k                                      D．无法确定

[变式训练2-4]真空中两个点电荷相距为r时，它们间的静电力大小为F；如果保持它们的电荷量不变，而将距离增大为2r，则静电力大小将变为(　　)

A．2F　　　　B．F　　　　C.　　　　D.

[变式训练2-5] (多选)半径相同的两个金属小球A、B带有相等的电荷量，相隔一定的距离，今让第三个半径相同的不带电的金属小球先后与A、B接触后移开。这时，A、B两球的电荷量之比可能为(　　)

A．2∶3　                                          B．3∶2

C．2∶1                                              D．1∶2

 

▲反思总结

1. 用公式计算静电力时，不必代入q的正、负号，力是矢量，正负号代表方向，我们按照绝对值算出大小，方向根据同性相斥，异性相吸，判断说明即可。

2．在研究微观粒子时，由于微观粒子间的万有引力远小于库仑力，所以一般把万有引力忽略。

3．电荷分配规律：两个完全相同的导体球相互接触，若两导体球带同种电荷，会把总电荷量平分；若带异种电荷，则先中和然后再把剩余电荷量平分。

 

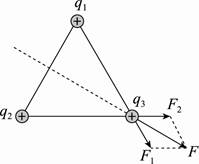
任务三：静电力的叠加

[例3]真空中有三个带正电的点电荷，它们固定在边长50 cm 的等边三角形的三个顶点上，每个点电荷都是2×10^－6 C，求它们各自所受的静电力。

q₃共受F₁和F₂两个力的作用，q₁＝q₂＝q₃＝q，相互距离r都相同，所以

 

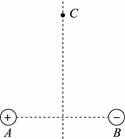
F₁＝F₂＝k＝ N＝0.144 N

根据平行四边形定则，合力是

F＝2F₁cos 30°＝0.25 N

合力的方向沿q₁与q₂连线的垂直平分线向外．

[变式训练3-1]如图所示，分别在A、B两点放置点电荷Q₁＝＋2×10^－14 C和Q₂＝－2×10^－14 C．在AB的垂直平分线上有一点C，且AB＝AC＝BC＝6×10^－2 m．如果有一高能电子静止放在C点处，则它所受的库仑力的大小和方向如何？

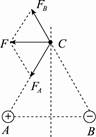
解析：电子带负电荷，在C点同时受A、B两点电荷的作用力F_A、F_B，如图所示．

由库仑定律F＝k得F_A＝k＝

9.0×10⁹× N＝8.0×10^－21 N

F_B＝k＝8.0×10^－21 N

由矢量的平行四边形定则和几何知识得静止放在C点的高能电子受到的库仑力F＝F_A＝F_B＝8.0×10^－21 N，方向平行于AB连线由B指向A.

 

 

 

 

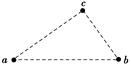
[变式训练3-2]如图所示，三个固定的带电小球a、b和c，相互间的距离分别为ab＝5 cm，bc＝3 cm，ca＝4 cm。小球c所受库仑力的合力的方向平行于a、b的连线。设小球a、b所带电荷量的比值的绝对值为k，则(　　)

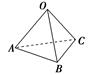
A．a、b的电荷同号，k＝

B．a、b的电荷异号，k＝

C．a、b的电荷同号，k＝

D．a、b的电荷异号，k＝

[变式训练3-3]水平面上A、B、C三点固定着三个电荷量为Q的正点电荷，将另一质量为m的带正电的小球(可视为点电荷)放置在O点，OABC恰构成一棱长为L的正四面体，如图所示。已知静电力常量为k，重力加速度为g，为使小球能静止在O点，小球所带的电荷量为(　　)

A．　　　

B．

C． 

D．