学习物理网移动版

第2节　动量定理

知识点归纳

知识点一、冲量

(1)概念：力与力的作用时间的乘积叫做力的冲量．

(2)定义式：I＝Ft.

(3)物理意义：冲量是反映力的作用对时间的累积效应的物理量，力越大，作用时间越长，冲量就越大．

(4)单位：在国际单位制中，冲量的单位是牛·秒，符号为 N·s.

知识点二、冲量的理解

(1)冲量的绝对性．由于力和时间均与参考系无关，所以力的冲量也与参考系的选择无关．

(2)冲量是矢量．冲量的运算服从平行四边形定则，合冲量等于各外力的冲量的矢量和，若整个过程中，不同阶段受力不同，则合冲量为各阶段冲量的矢量和．

(3)冲量是过程量，它是力在一段时间内的积累，它取决于力和时间这两个因素．所以求冲量时一定要明确所求的是哪一个力在哪一段时间内的冲量．

知识点三、冲量的计算

(1)恒力的冲量：公式 I＝Ft 适用于计算某个恒力的冲量，这时冲量的数值等于力与作用时间的乘积，冲量的方向与恒力方向一致．若力为同一方向均匀变化的力，该力的冲量可以用平均力计算，若力为一般变力则不能直接计算冲量．

(2)变力的冲量

①变力的冲量通常可利用动量定理 I＝Δp 求解．

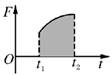
②可用图象法计算如图所示变力冲量，若某一力方向恒定不变，那么在 F－t 图象中，图中阴影部分的面积就表示力在时间Δt＝t2－t1 内的冲量．

知识点四、冲量与功

(1)联系：冲量和功都是力作用过程的积累，是过程量．

(2)区别：冲量是矢量，是力在时间上的积累，具有绝对性；功是标量，是力在位移上的积累，有相对性．

知识点四、动量定理

1．内容：物体在一个过程始末的动量变化量等于它在这个过程中所受力的冲量．这个关系叫做动量定理．

2．表达式：I＝Δp 或 Ft＝mv′－mv.

3．对动量定理的理解

(1)动量定理反映了合外力的冲量是动量变化的原因．

(2)动量定理的表达式是矢量式，它说明合外力的冲量跟物体动量变化量不仅大小相等，而且方向相同．

(3)动量的变化率和动量的变化量由动量定理可得出F＝，它说明动量的变化率决定于物体所受的合外力．而由动量定理 I＝Δp 可知动量的变化量取决于合外力的冲量，它不仅与物体的受力有关，还与力的作用时间有关．

(4)动量定理具有普遍性，即不论物体的运动轨迹是直线还是曲线，不论作用力是恒力还是变力，不论几个力的作用时间是相同还是不同都适用．

4．动量定理的应用

(1)定性分析有关现象由F＝可知：

①Δp 一定时，t 越小，F 越大；t 越大，F 越小．

②Δp 越大，而 t 越小，F 越大．

③Δp 越小，而 t 越大，F 越小．

(2)应用动量定理解决问题的一般步骤

①审题，确定研究对象：对谁、对哪一个过程．

②对物体进行受力分析，分析力在过程中的冲量，或合力

在过程中的冲量．

③抓住过程的初、末状态，选定参考方向，对初、末状态的动量大小、方向进行描述．

④根据动量定理，列出动量定理的数学表达式．

⑤写清各物理量之间关系的补充表达式．

⑥求解方程组，并分析作答．

典例分析

一、冲量的理解

例1  如图所示，质量为 m 的小球由高为 H 的光滑固定斜面顶端无初速滑到底端过程中，重力、弹力的冲量各是多大？

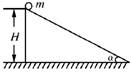
解析 重力、弹力两个力的作用时间都是t＝＝，力的大小依次是mg、mgcos α，所以它们的冲量依次是：I_G＝，I_N＝.

答案     

二、平均冲量的计算

例2  如图所示，质量为 m＝1 kg 的小球由高 h1＝0.45 m处自由下落，落到水平地面后，反弹的最大高度为 h2＝0.2 m，从小球下落到反弹到最高点经历的时间为Δt＝0.6 s，g 取 10 m/s2.求：小球撞击地面过程中，球对地面的平均压力 F 的大小．

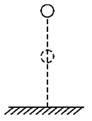
解析 以小球为研究对象，从开始下落到反弹到最高点的全过程动量变化为零，根据下降、上升高度可知其中下落、上升分别用时 t1＝0.3 s 和t2＝0.2 s，因此与地面作用的时间必为 t3＝0.1 s．由动量定理得：mgΔt－Ft3＝0 代入数据解得 F＝60 N.

答案 60 N

三、合力冲量的计算

例3  质量为1.0 kg的小球从20 m高处自由下落到软垫上，反弹后上升的最大高度为5.0 m，小球与软垫接触时间为1.0 s，在接触时间内小球受到的合力的冲量大小为(空气阻力不计，g＝10 m/s2)(　　)

A．10 N·s　　　　　　B．20 N·s      C．30 N·s          D．40 N·s

解析 小球从开始下落到落到软垫上过程中，由动能定理可得：mgh₁＝mv－0，

代入数据解得：v₁＝20 m/s, 方向竖直向下；

小球从反弹到到达最高点过程中：－mgh₂＝0－mv，

代入数据解得：v₂＝10 m/s，方向竖直向上；

以竖直向上为正方向，由动量定理得：

I＝mv₂－mv₁＝1×10 kg·m/s－1×(－20) kg·m/s＝30 kg·m/s＝30 N·s，

方向竖直向上；故选C.

答案 C

归纳总结：对于动量定理的应用，要注意其中各量的方向性，正确设定正方向，确定各量的正负．

四、冲量的综合应用

例4  用0．5kg的铁锤把钉子钉进木头里，打击时铁锤的速度v＝4.0m/s，如果打击后铁锤的速度变为0，打击的作用时间是0.01s，那么：

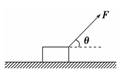
(1)不计铁锤受的重力，铁锤钉钉子的平均作用力是多大？

(2)考虑铁锤受的重力，铁锤钉钉子的平均作用力又是多大？(g取10m/s²)

(3)比较(1)和(2)，讨论是否要计铁锤的重力。

解析 (1)以铁锤为研究对象，不计重力时，只受钉子的作用力，方向竖直向上，设为F₁，取竖直向上为正，由动量定理可得F₁t＝0－mv

所以F₁＝－N＝200N，方向竖直向上。

由牛顿第三定律知铁锤钉钉子的作用力为200N，方向竖直向下。

(2)若考虑重力，设此时受钉子的作用力为F₂，对铁锤应用动量定理，取竖直向上为正。

(F₂＋mg)t＝0－mv(矢量式)

F₂＝N－0.5×(－10)N＝205N，方向竖直向上。

由牛顿第三定律知，此时铁锤钉钉子的作用力为205N，方向竖直向下。

(3)比较F₁与F₂，其相对误差为×100%＝2.5%，可见本题中重力的影响可忽略。

答案 (1)200N，方向竖直向下　(2)205N，方向竖直向下　(3)见解析

自我检测

1．关于冲量，下列说法正确的是(　　)

A．冲量是物体动量变化的原因

B．作用在静止物体上的力的冲量一定为零

C．动量越大的物体受到的冲量越大

D．冲量的方向就是物体受力的方向

解析 力作用一段时间便有了冲量，而力作用一段时间后，物体的运动状态发生了变化，物体的动量就发生了变化．因此说冲量是物体动量变化的原因，A选项正确；只要有力作用在物体上，经历一段时间，这个力便有了冲量I＝Ft，与物体处于什么状态无关，物体运动状态的变化情况是所有作用在物体上的力共同产生的效果，所以B选项不正确；物体所受冲量I＝Ft与物体的动量的大小p＝mv无关，C选项不正确；冲量是一个过程量，只有在某一过程中力的方向不变时，冲量的方向才与力的方向相同，故D选项不正确．

答案  A

2．篮球运动员通常伸出双手迎接传来的篮球．接球时，两手随球迅速收缩至胸前．这样做可以(　　)

A．减小球对手的冲量

B．减小球对人的冲击力

C．减小球的动量变化量

D．减小球的动能变化量

解析  接球过程中，球的初动量和末动量一定，所以球的动量变化量恒定不变，选项C错误；根据动量定理，手对球的冲量等于球动量的改变量，也恒定不变，球对手的冲量也不变，选项A错误；球的初动能和末动能一定，所以球的动能变化量恒定不变，选项D错误；根据动量定理I＝Ft，球对手的冲量I不变，接球时两手随球迅速收缩至胸前，是通过延长受力时间以减小球对人的冲击力F，所以选项B正确．

答案  B

3．如图所示，一个物体在与水平方向成θ角的拉力F的作用下匀速前进了时间t，则(　　)

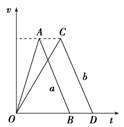
A．拉力F对物体的冲量大小为Ft

B．拉力对物体的冲量大小为Ftsin θ

C．摩擦力对物体的冲量大小为Ftsin θ

D．合外力对物体的冲量大小为零

解析 求冲量时，必须明确是哪一个力在哪一段时间内的冲量．本题中，作用的时间都是一样的，求力F对物体的冲量就是Ft，所以A项正确、B项错误；物体受到的摩擦力F_f＝Fcos θ，所以摩擦力对物体的冲量大小为F_ft＝Fcos θt，C项错；物体做匀速运动，合外力为零，所以合外力对物体的冲量大小为零，D对．正确选项为A、D.

答案 AD

4．一位质量为m的运动员从下蹲状态向上起跳，经Δt时间，身体伸直并刚好离开地面，速度为v.在此过程中(　　)

A．地面对他的冲量为mv＋mg·Δt，地面对他做的功为mv²

B．地面对他的冲量为mv＋mg·Δt，地面对他做的功为零

C．地面对他的冲量为mv，地面对他做的功为mv²

D．地面对他的冲量为mv－mg·Δt，地面对他做的功为零

解析 首先，由动量定理可知，合外力的冲量等于运动员动量的改变量，有表达式I_G＋I_F＝Δp，即－mg·Δt＋I_F＝mv－0，I_F＝mv＋mg·Δt，地面对运动员的作用力只有支持力，所以地面对运动员的冲量为mv＋mg·Δt，排除C、D选项；另外，由于地面对运动员的支持力的作用点未发生位移，所以支持力对运动员不做功，故该题正确选项为B.

答案 B

5．从同样高度落下的玻璃杯，掉在水泥地上容易打碎，而掉在草地上不容易打碎，其原因是(　　)

A．掉在水泥地上的玻璃杯动量小，而掉在草地上的玻璃杯动量大

B．掉在水泥地上的玻璃杯动量改变小，掉在草地上的玻璃杯动量改变大

C．掉在水泥地上的玻璃杯动量改变大，掉在草地上的玻璃杯动量改变小

D．掉在水泥地上的玻璃杯与地面接触时作用力大，而掉在草地上的玻璃杯与地面接触时作用力小

解析 玻璃杯从同样高度落下，到达地面时具有相同的速度，即具有相同的动量，与地面相互作用后都静止．所以两种地面的情况中玻璃杯动量的改变量相同，故A、B、C错误；落在水泥地上时，作用时间短，故作用力大，落在草地上时，作用时间长，故作用力小，故D正确．

答案 D

6．水平推力F₁和F₂分别作用在水平面上等质量的a、b两物体上，作用一段时间后撤去推力，物体将继续运动一段时间后停下，两物体vt的图象如图所示，图中AB∥CD，则(　　)

A．F₁的冲量大于F₂的冲量           

B．F₁的冲量等于F₂的冲量

C．两物体受到的摩擦力大小相等

D．两物体受到的摩擦力大小不等

解析 设F₁、F₂的作用时间分别为t₁、t₂，则由图知t₁＜t₂，当只有摩擦力F_f作用时，由AB∥CD知图线斜率相同，则加速度相等，由牛顿第二定律知，摩擦力F_f相等，故C选项正确，D选项错误．对a，由动量定理得：F₁t₁－F_ft₁＝mv_A；对b同理得：F₂t₂－F_ft₂＝mv_C.由图象知，v_A＝v_C，t₁＜t₂，所以由mv_A＝mv_C知，即F₁t₁－F_ft₁＝F₂t₂－F_ft₂，因此F₁t₁＜F₂t₂，即A正确，B错误．

答案 AC

7．古时有“守株待兔”的寓言，设兔子的头部受到大小等于自身体重的撞击力时即可致死。若兔子与树桩发生碰撞，作用时间为0.2 s，则撞死的兔子的奔跑速度可能是(　　)

A．1 m/s  B．1.5 m/s  C．2 m/s  D．2.5 m/s

解析　设兔子与树桩的撞击力为F，兔子撞击后速度为零，根据动量定理有Ft＝mv，所以，v＝≥＝gt＝2 m/s，选项CD正确．

答案　CD

8．人们常说“滴水穿石”，请你根据下面所提供的信息，估算水对石头的冲击力的大小．一瀑布落差为h＝20 m，水流量为Q＝0.10 m³/s，水的密度ρ＝1.0×10³ kg/m³，水在最高点和落至石头上后的速度都认为是零．(落在石头上的水立即流走，在讨论石头对水的作用时可以不考虑水的重力，g取10 m/s²)

解析　设水滴下落与石头碰前速度为v，则有mgh＝mv²

设时间Δt内有质量为Δm的水冲到石头上，石头对水的作用力为F，由动量定理得：－FΔt＝0－Δmv又因Δm＝ρQΔt

联立得：F＝ρQ＝2×10³ N

由牛顿第三定律，水对石头的作用力：F′＝F＝2×10³ N，方向竖直向下．

答案　2×10³ N

9．质量为60 kg的建筑工人，不慎从高空跌下，由于弹性安全带的保护，使他悬挂起来．已知弹性安全带的缓冲时间是1.2 s，安全带长5 m，g取10 m/s²，则安全带所受的平均冲力的大小是多少？

解析 选取人为研究对象，人下落过程中由：v²＝2gh，得：v＝＝10 m/s，

以竖直向上为正方向，缓冲过程由动量定理得：

(F－mg)t＝mv，得：F＝＋mg＝1 100 N.

由牛顿第三定律可知，安全带所受的平均冲力大小为1 100 N.

答案 安全带所受的平均冲力大小为1 100 N.

10．一辆轿车强行超车时，与另一辆迎面驶来的轿车相撞，两车相撞后连为一体，两车车身因相互挤压，皆缩短了0.5 m，据测算两车相撞前的速度均约为30 m/s，求：

(1)若人与车一起做减速运动，车祸过程中车内质量约60 kg的人受到的平均冲力是多大？

(2)若此人系有安全带，安全带在车祸过程中与人体作用时间是1 s，求这时人体受到的平均冲力为多大？

解析 (1)两车相撞时认为人与车一起做匀减速运动直至停止，位移为0.5 m.

设运动时间为t，根据x＝t，得t＝＝ s

根据动量定理Ft＝Δp＝mv₀，

得F＝＝ N＝5.4×10⁴ N.

(2)若人系有安全带，则F＝＝ N＝1.8×10³ N.

答案 (1)5.4×10⁴ N　(2)1.8×10³ N