第3讲 光的折射 全反射
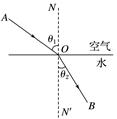
一、光的折射定律 折射率 1.折射定律 (1)内容:如图1所示,折射光线与入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比.
图1 (2)表达式:=n. (3)在光的折射现象中,光路是可逆的. 2.折射率 (1)折射率是一个反映介质的光学性质的物理量. (2)定义式:n=. (3)计算公式:n=,因为v<c,所以任何介质的折射率都大于1. (4)当光从真空(或空气)射入某种介质时,入射角大于折射角;当光由介质射入真空(或空气)时,入射角小于折射角. 3.折射率的理解 (1)折射率由介质本身性质决定,与入射角的大小无关. (2)折射率与介质的密度没有关系,光密介质不是指密度大的介质. (3)同一种介质中,频率越大的色光折射率越大,传播速度越小.
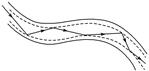
(1)光的传播方向发生改变的现象叫光的折射.( × ) (2)折射率跟折射角的正弦成正比.( × ) (3)光从空气射入水中,它的传播速度一定增大.( × ) (4)在同一种介质中,光的频率越大,折射率越大.( √ ) 二、全反射 光导纤维 1.定义:光从光密介质射入光疏介质,当入射角增大到某一角度时,折射光线将全部消失,只剩下反射光线的现象. 2.条件:(1)光从光密介质射入光疏介质.(2)入射角大于或等于临界角. 3.临界角:折射角等于90°时的入射角.若光从光密介质(折射率为n)射向真空或空气时,发生全反射的临界角为C,则sin C=.介质的折射率越大,发生全反射的临界角越小. 4.光导纤维 光导纤维的原理是利用光的全反射.如图2所示.
图2
(1)光密介质和光疏介质是相对而言的.同一种介质,相对于其他不同的介质,可能是光密介质,也可能是光疏介质.( √ ) (2)如果光线从光疏介质进入光密介质,则无论入射角多大,都会发生全反射现象.( × ) (3)在光的反射和全反射现象中,均遵循光的反射定律,光路均是可逆的.( √ ) (4)当光射到两种介质的界面上时,往往同时发生光的折射和反射现象,在全反射现象中,也是如此.( × )
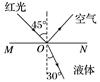
1.(人教版选修3-4P53第1题)(多选)光从介质a射向介质b,如果要在a、b介质的分界面上发生全反射,那么必须满足的条件是( ) A.a是光密介质,b是光疏介质 B.光在介质a中的速度必须大于在介质b中的速度 C.光的入射角必须大于或等于临界角 D.必须是单色光 答案 AC 2.一束单色光经空气射入玻璃,这束光的( ) A.速度变小,波长变短 B.速度不变,波长变短 C.频率增大,波长变长 D.频率不变,波长变长 答案 A 3.如图3所示,MN是空气与某种液体的分界面,一束红光由空气射到分界面,一部分光被折射,一部分光进入液体中.当入射角是45°时,折射角为30°,则以下说法正确的是( )
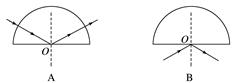
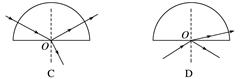
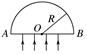
图3 A.反射光线与折射光线的夹角为120° B.该液体对红光的折射率为 C.该液体对红光的全反射临界角为45° D.当紫光以同样的入射角从空气射到分界面时,折射角也是30° 答案 C 4.(多选)关于折射率,下列说法正确的是( ) A.根据n=可知,介质的折射率与入射角的正弦成正比 B.根据n=可知,介质的折射率与折射角的正弦成反比 C.根据n=可知,介质的折射率与光在该介质中的速度成反比 D.同一频率的光由真空进入某种介质时,折射率与光在介质中的波长成反比 答案 CD 5.如图,一束光由空气射向半圆柱体玻璃砖,O点为该玻璃砖截面的圆心,下图能正确描述其光路的是( )
答案 A
命题点一 折射定律和折射率的理解及应用 1.对折射率的理解 (1)折射率大小不仅反映了介质对光的折射本领,也反映了光在介质中传播速度的大小v=. (2)折射率的大小不仅与介质本身有关,还与光的频率有关.同一种介质中,频率越大的色光折射率越大,传播速度越小. (3)同一种色光,在不同介质中虽然波速、波长不同,但频率相同. 2.光路的可逆性 在光的折射现象中,光路是可逆的.
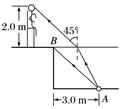
图4 (1)求池内的水深; (2)一救生员坐在离池边不远处的高凳上,他的眼睛到池面的高度为2.0 m.当他看到正前下方的点光源A时,他的眼睛所接受的光线与竖直方向的夹角恰好为45°.求救生员的眼睛到池边的水平距离(结果保留1位有效数字).
答案 (1) m (2)0.7 m 解析 (1)光由A射向B发生全反射,光路如图甲所示.
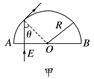
甲 则sin θ= 得sin θ= 由|AO|=3 m,由几何关系可得: |AB|=4 m,|BO|= m 所以水深 m. (2)光由A点射入救生员眼中光路图如图乙所示.
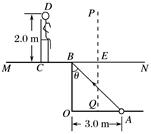
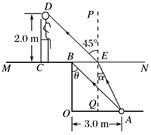
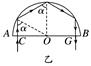
乙 由折射定率n= 可知sin α= tan α= 设|BE|=x,得tan α== 代入数据得x=(3-) m≈1.3 m, 由几何关系得,救生员的眼睛到池边的水平距离为 |BC|=(2-x) m≈0.7 m
解决光的折射问题的思路 1.根据题意画出正确的光路图. 2.利用几何关系确定光路中的边、角关系,要注意入射角、折射角均以法线为标准. 3.利用折射定律、折射率公式求解. 4.注意:在折射现象中光路是可逆的.
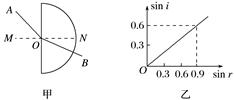
1.某同学通过实验测定半圆形玻璃砖的折射率n.如图5甲所示,O是圆心,MN是法线,AO、BO分别表示某次测量时光线在空气和玻璃砖中的传播路径.该同学测得多组入射角i和折射角r,作出sin isin r图象如图乙所示.则( )
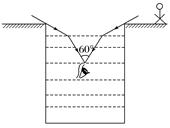
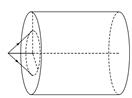
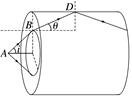
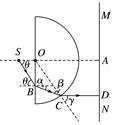
图5 A.光由A经O到B,n=1.5 B.光由B经O到A,n=1.5 C.光由A经O到B,n=0.67 D.光由B经O到A,n=0.67 答案 B 解析 介质折射率的计算为空气中的角度和介质中角度的正弦值之比,空气中角度较大,对应正弦值较大,对应题图中折射角r,故OA为折射光线,光线从B经O到A, 由折射率计算公式得n===1.5,故选项B正确,A、C、D错误. 2.如图6所示,某潜水员在检查装有透明液体的圆柱体容器,当潜水员的眼睛在容器中心轴位置且在液面下h2=1 m处时,他看到容器口处所有景物都出现在一个顶角为60°的倒立圆锥里,已知容器口距离液面的距离h1=1 m,圆柱体的横切面半径r= m.
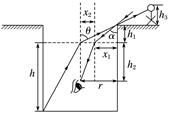
图6 (1)求容器中液体的折射率; (2)若有一个身高h3=1 m的小孩站在离容器口边缘x= m远的位置,小孩恰好能看到对面的容器底部,则容器中液体的深度约为多少? 答案 (1) (2) m 解析 (1)由几何关系可得:=tan α;=tan 30° 其中x1+x2=r 解得:tan α=,n= 解得:n=
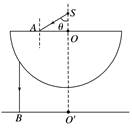
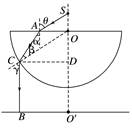
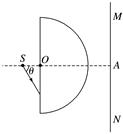
(2)由几何关系可知,光从容器底部射入小孩眼睛时 折射角的正切值tan θ== 入射角的正切值tan β= 由折射定律可知=n= 解得:h= m. 3.如图7所示,将半径为R的透明半球体放在水平桌面上方,O为球心,直径恰好水平,轴线OO′垂直于水平桌面.位于O点正上方某一高度处的点光源S发出一束与OO′夹角θ=60°的单色光射向半球体上的A点,光线通过半球体后刚好垂直射到桌面上的B点,已知O′B=R,光在真空中传播速度为c,不考虑半球体内光的反射,求:
图7 (1)透明半球体对该单色光的折射率n; (2)该光在半球体内传播的时间. 答案 (1) (2) 解析 (1)光从光源S射出经半球体到达水平桌面的光路如图.
光由空气射向半球体,由折射定律,有n=,在△OCD中,sin∠COD= 得∠COD=60° 由几何知识知γ=∠COD=60° 光由半球体射向空气,由折射定律,有n= 故α=β 由几何知识得α+β=60° 故α=β=30° 解得n= (2)光在半球体中传播的速度为v==c 由几何关系知AC=AO 且ACsin α+AO=O′B 得AC=R 光在半球体中传播的时间t==. 命题点二 全反射现象的理解和综合分析 1.分析综合问题的基本思路 (1)判断光线是从光疏介质进入光密介质还是从光密介质进入光疏介质. (2)判断入射角是否大于临界角,明确是否发生全反射现象. (3)画出反射、折射或全反射的光路图,必要时还可应用光路的可逆原理画出光路图,然后结合几何知识进行推断和求解相关问题. (4)折射率n是讨论折射和全反射问题的重要物理量,是联系各物理量的桥梁,对跟折射率有关的所有关系式应熟练掌握. 2.求光的传播时间的一般思路 (1)全反射现象中,光在同种均匀介质中的传播速度不发生变化,即v=. (2)全反射现象中,光的传播路程应结合光路图与几何关系进行确定. (3)利用t=求解光的传播时间.
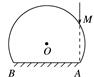
图8 (1)一束平行光垂直射向玻璃砖的下表面,若光线到达上表面后,都能从该表面射出,则入射光束在AB上的最大宽度为多少? (2)一细束光线在O点左侧与O相距R处垂直于AB从下方入射,求此光线从玻璃砖射出点的位置. 答案 见解析 解析 (1)在
O点左侧,设从E点射入的光线进入玻璃砖后在上表面的入射角恰好等于全反射的临界角θ,则OE区域的入射光线经上表面折射后都能从玻璃砖射出,如图甲.由全反射条件有 sin θ=① 由几何关系有 OE=Rsin θ② 由对称性可知,若光线都能从上表面射出,光束的宽度最大为l=2OE③ 联立①②③式,代入已知数据得 l=R④ (2)设光线在距O点R的C点射入后,在上表面的入射角为α,由几何关系及①式和已知条件得 α=60°>θ⑤
光线在玻璃砖内会发生三次全反射,最后由G点射出,如图乙,由反射定律和几何关系得 OG=OC=R⑥ 射到G点的光有一部分被反射,沿原路返回到达C点射出.
解答全反射类问题的技巧 1.根据题意画出光的折射或恰好发生全反射的光路图. 2.作图时找出具有代表性的光线,如符合边界条件的临界光线等. 3.利用平面几何知识分析线、角关系,找出入射角、折射角或临界角.注意入射角、折射角均以法线为标准. 4.以刚好发生全反射的光线为比较对象,来判断光线是否发生全反射,从而画出其他光线的光路图.
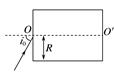
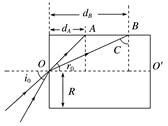
4.半径为R、介质折射率为n的透明圆柱体,过其轴线OO′的截面如图9所示.位于截面所在平面内的一细束光线,以角i0由O点入射,折射光线由上边界的A点射出.当光线在O点的入射角减小至某一值时,折射光线在上边界的B点恰好发生全反射.求A、B两点间的距离.
图9 答案 R 解析 当光线在O点的入射角为i0时,设折射角为r0,由折射定律得=n①
设A点与左端面的距离为dA,由几何关系得 sin r0=② 若折射光线恰好发生全反射,则在B点的入射角恰好为临界角C,设B点与左端面的距离为dB,由折射定律得 sin C=③ 由几何关系得 sin C=④ 设A、B两点间的距离为d,可得 d=dB-dA⑤ 联立①②③④⑤式得 d=R. 5.如图10所示,有一玻璃圆柱体,横截面半径为R=10 cm,长为L=100 cm.一点光源在玻璃圆柱体中心轴线上的A点,与玻璃圆柱体左端面距离d=4 cm,点光源向各个方向发射单色光,其中射向玻璃圆柱体从左端面中央半径为r=8 cm圆面内射入的光线恰好不会从柱体侧面射出.光速为c=3×108 m/s;求:
图10 (1)玻璃对该单色光的折射率; (2)该单色光通过玻璃圆柱体的最长时间. 答案 (1) (2)6×10-9 s 解析 (1)由题意可知,光线AB从圆柱体左端面射入,在柱体侧面发生全反射.
sin i== n= sin C= sin θ=cos C= 得n= (2)折射光BD在玻璃圆柱体内传播路程最长,因而传播时间最长. s==nL v= t===6×10-9 s.
题组1 光的折射和折射率 1.如图1所示,一个半径为R、折射率为的透明玻璃半球体,O为球心,轴线OA水平且与半球体的左边界垂直,位于轴线上O点左侧处的点光源S发出一束与OA夹角θ=60°的光线射向半球体,已知光在真空中传播的速度为c.求:光线第一次从玻璃半球体射出时的方向以及光线在玻璃半球体内传播的时间.
图1 答案 见解析 解析 作出大致光路图如图所示,由几何知识可得
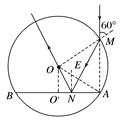
lOB=tan θ= 又n== 解得:α=30° 在△OBC中有:= 解得:β=30° 又n== 解得γ=60° 则知出射光线CD方向与OA平行 光在玻璃半球体中传播的距离lBC=lOB 又速度v= 可得:t==. 2.如图2所示,玻璃球冠的折射率为,其底面镀银,底面的半径是球半径的倍;在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的M点,该光线的延长线恰好过底面边缘上的A点,求该光线从球面射出的方向相对于其初始入射方向的偏角.
图2 答案 150° 解析 设图中N点为光线在球冠内底面上的反射点,光线的光路图如图所示.设光线在M点的入射角为i、折射角为r,在N点的入射角为i′,反射角为i″,玻璃折射率为n.由于△OAM为等边三角形,
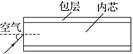
i=60°① 由折射定律有 sin i=nsin r② 代入题给条件n=得 r=30°③ 作底面在N点的法线NE,由于NE∥AM,有 i′=30°④ 根据反射定律,有 i″=30°⑤ 连接ON,由几何关系知△MAN≌△MON,故有 ∠MNO=60°⑥ 由④⑥式得 ∠ENO=30° 于是∠ENO为反射角,NO为反射光线.这一反射光线经球面再次折射后不改变方向.所以,经一次反射后射出玻璃球冠的光线相对于入射光线的偏角β为 β=180°-∠ENO=150°. 题组2 光的全反射现象分析 3.如图3所示,光导纤维由内芯和包层两个同心圆柱体组成,其中心部分是内芯,内芯以外的部分为包层,光从一端进入,从另一端射出,下列说法正确的是( )
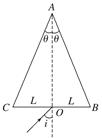
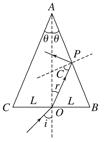
图3 A.内芯的折射率大于包层的折射率 B.内芯的折射率小于包层的折射率 C.不同频率的可见光从同一根光导纤维的一端传输到另一端所用的时间相同 D.若紫光以如图所示角度入射时,恰能在内芯和包层分界面上发生全反射,则改用红光以同样角度入射时,也能在内芯和包层分界面上发生全反射 答案 A 4.如图4所示,三角形ABC为某透明介质的横截面,O为BC边的中点,位于截面所在平面内的一束光线自O以角i入射,第一次到达AB边恰好发生全反射.已知θ=15°,BC边长为2L,该介质的折射率为,求:
图4 (1)入射角i; (2)从入射到发生第一次全反射所用的时间(设光在真空中的速度为c,可能用到:sin 75°=或tan 15°=2-). 答案 (1)45° (2) 解析 (1)如图所示,根据全反射规律可知,光线在AB面上P点的入射角等于临界角C,由折射定律得 sin C=① 代入数据得C=45°②
设光线在BC面上的折射角为r,由几何关系得 r=30°③ 由折射定律得 n=④ 联立③④式,代入数据得 i=45°⑤ (2)在△OPB中,根据正弦定理得 =⑥ 设所用时间为t,光线在介质中的速度为v,得 =vt⑦ v=⑧ 联立⑥⑦⑧式,代入数据得t=L
|